研究背景与问题定义 [page::0][page::1]

• 超声空化气泡的非线性振荡是化学合成、乳化等多种超声应用基础。

- 多气泡系统中气泡间相互作用复杂，传统单泡模型难以准确描述气泡动力学。

• 论文旨在通过VOF数值模拟揭示多泡环境下气泡振荡幅度增强的机理。

数值模型与计算条件 [page::1][page::2][page::3]

• 使用OpenFOAM实现可压缩流体多相VOF方法，计算域为400μm立方体，中央气泡初始直径20μm。

- 多种多泡构型：四面体、六面体、八面体，包围气泡距中心气泡100-150μm。

• 求解动量、质量和能量守恒方程，边界施加20kHz正弦声压，振幅分别取0.5、0.7、0.9atm。

- 自适应网格细化技术(AMR)保证气泡边界区高分辨率。

多泡系统下气泡振荡增强的数值结果 [page::3][page::4]

• 多泡系统中心气泡压力振荡幅度和气泡半径明显高于单泡系统，且随包围气泡数量增加而增强。

• 观察到多泡环境导致相位滞后，中心气泡压缩显著滞后，扩展更大，液体射流从包围气泡指向中心气泡。

声栉效应(acoustic wake effect)机制及定量分析 [page::4][page::5][page::6]

• 声压场模拟显示周围气泡遮蔽声波，降低中心气泡附近压力，形成声栉效应，产生明显的声波传播延迟。

- 提出覆盖率(cover ratio)参数，定义为包围气泡投影面积与球面面积比，定量描述声栉效应强度。

• 覆盖率与中心气泡最小压力、最大半径和振幅时间延迟均呈线性正相关。

| R/μm | Polyhedron | r_cov (-) |
|-------|------------|-----------|
| 100 | 4 | 0.04000 |
| 150 | 4 | 0.01778 |
| 100 | 6 | 0.08000 |
| 150 | 6 | 0.03556 |
| 100 | 8 | 0.06000 |
| 150 | 8 | 0.02667 |

声栉效应对气泡振荡具体影响与验证 [page::7][page::8]

• 中心气泡内外压力及半径时间演化显示，多泡环境使超声传播延迟，导致中心气泡扩展更大，压缩更剧烈。

• 多泡系统中中心气泡振荡幅度最大，包围气泡也高于单泡系统。

• 包围气泡压缩产生的压力波对中心气泡振荡影响有限，声栉效应主导振荡增强。

理论模型对声速变化的支持及研究意义 [page::9]

• 通过改进声速公式结合泡体体积分数，解释传播速度降低和声压衰减。

- 覆盖率参数弥补了单纯考虑包围气泡数量的不足，更全面评估多泡振荡影响。

• 结果表明需在Rayleigh-Plesset等模型中引入声栉效应及相位延迟以提高气泡动力学预测精度。

报告深度分析报告

一、元数据与概览

报告标题：
Enhancement of oscillation amplitude of cavitation bubble due to acoustic wake effect in multibubble environment

作者与机构：
Takuya Yamamoto, Sergey V. Komarov
东北大学 环境研究研究科及工程研究科冶金系，宫城县，日本

发布日期与载体：
预印本/学术论文，具体发布日期未明，结合引用文献和软件版本推测为2020年前后。

主题领域：
该报告聚焦于超声波诱发空化气泡的多气泡系统中气泡振荡行为的数值模拟和物理机制分析，属于声学物理、流体力学及多相流研究范畴，尤其针对超声空化技术中气泡相互作用的影响机制。

核心论点、目标及创新点：

• 核心发现是多气泡环境下，空化气泡的振荡幅度会因邻近气泡的存在而明显增强，提升甚至超过单个气泡的振荡幅度。

- 作者通过数值模拟揭示这是“声学尾流效应（acoustic wake effect）”导致的，该效应使气泡附近压力下降，同时使得气泡振荡的收缩与膨胀周期与声压振荡之间出现时间延迟，从而放大振荡幅度。

• 创新之处在于引入“遮蔽比（cover ratio）”参数，用以量化相邻气泡对中心气泡振荡幅度、时间延迟及最大半径的影响。

- 使用基于OpenFOAM的可压缩性代数体积分数（VOF）多相流模型，大幅提升了对复杂多气泡交互的解析精度，尤其克服了以往基于Rayleigh-Plesset方程间接模拟中未考虑声波遮蔽与传播延迟的问题。

总体而言，作者旨在用高保真数值模型阐明多气泡环境下气泡振荡幅度增强的物理机制，为超声空化应用中气泡群动力学提供理论基础和数值参考 [page::0,1]。

---

二、逐节深度解读

1. 引言

• 关键论点：

超声波激发的空化空泡在化学合成、清洗、雾化、乳化等领域产生显著效应，其本质在于气泡的非线性振荡。过去多集中于单气泡振荡行为研究，但实际工业应用几乎总存在多气泡体系，其间气泡交互导致诸多独特现象，如气泡簇形成、声压超过阈值时声化学效率降低、声波产生次谐波等。然而，气泡间具体的交互机制仍未被充分揭示，尤其实验上难直接观测大量气泡的相互作用。

• 理论背景与研究空白：

介绍了Rayleigh-Plesset和Keller方程在单气泡振荡中的应用及发展，指出多气泡系统中的复杂相互作用尚无统一数值或理论模型清晰描述，强调本研究通过数值模拟填补该空白的重要性。

• 作者立场与研究目标：

旨在通过数值模拟直观揭示多气泡系统中气泡振荡增强的原因，尤其捕捉气泡振荡间的时间相移和保护效应，进而引入定量评估参数“遮蔽比” [page::0]

2. 数值分析方法

2.1 计算条件和几何模型

• 模拟域为400微米立方体，中央放置主空泡（初始直径20微米），周围分布4~8个辅助气泡，位于规则多面体顶点（四面体、六面体、八面体），距离100~150微米，模拟不同气泡排列和间距对主气泡振荡影响。

- 声压以20kHz频率，0.5~0.9 atm幅度正弦波施加在边界，模拟实际超声激励。

• 假设流体为单相（空气-水），牛顿流体，无蒸发冷凝，气体密度按理想气体状态方程，浮力忽略。

- 这是高度理想化的模拟条件，适合揭示气泡动力学中的基本物理过程 [page::1]

2.2 主控制方程和多相流模型

• 求解不可压缩Navier-Stokes方程组中的动量、质量和能量守恒方程，具体方程视作多相流耦合求解，捕捉流体动力与热力学耦合效应。

- VOF方法捕捉气液界面演变，定义液体体积分数函数α；采用连续性方程传输体积分数，计算相间界面形态及界面张力。

• 表面张力通过连续表面力模型（CSF）实现，减少界面处虚假电流（spurious current）影响。表面张力和界面曲率通过拉普拉斯滤波处理，提高数值稳定性。

- 物理参数（密度、粘度、比热等）按体积分数加权平均 [page::2]

2.3 边界与初始条件

• 计算域边界施加自由进口出口速度边界，压力按照声压正弦波施加。

- 声波频率定为20kHz，声压幅度为0.5, 0.7, 0.9 atm三个梯度。

• 初始液体静止，温度300K，压力亚稳态考虑拉普拉斯压力校正。

- 各参数设计合理，保证模拟的物理一致性和数值稳定性 [page::2-3]

2.4 数值求解细节

• 自适应网格细化（AMR），初始网格间距2微米，细化区域1微米，保证气泡及界面捕捉精度。

- 时间步长根据库仑数限制在0.05以下确保求解稳定。

• 采用OpenFOAM v1812搭建求解框架，PISO算法耦合压力和速度。

- 模拟单周期需150小时，计算开销大，反映高度计算密集型 [page::3]

3. 结果与讨论

3.1 单气泡振荡特性及多气泡振荡增强

• 单气泡下，各声压幅度下气泡内压及等效半径时程显示：当声压低于0.5 atm，气泡线性振荡，振幅小稳定；超过0.7 atm，出现明显非线性振荡和相位滞后，振幅显著增加，球形变形明显。

- 多气泡环境中，中心气泡压力振荡幅度与等效半径均显著高于单气泡；且随着周围气泡数量增加，振幅增强更明显。

• 多气泡系统中，振荡相位出现延迟，气泡收缩时间被推迟，致使中心气泡保持扩展时间更长，振幅扩大。

- 模拟气泡形状变化揭示多气泡系统中气泡扩展相对更大，收缩延迟，声波与气泡振荡波动存在相位差，极大增强振幅。 [page::3,4]

3.2 声学尾流效应（Acoustic Wake Effect）分析

• 围绕中心气泡的压力场切片（20kHz，0.9 atm，周围气泡100微米距离排列）显示，中心气泡被周围气泡“遮蔽”，其周围声压显著低于单气泡情况，代表声波传播受阻。

- 该声波遮蔽即为“声学尾流效应”，导致中心气泡振荡晚于声压波动，膨胀时间延长，滚动压缩剧烈。

• 形成的液体喷射（jetting）效应也在模拟中被观察，体现多气泡动力学复杂性。

- 为定量描述，作者定义“遮蔽比”，即周围气泡在理论围绕中心气泡球面上的总投影面积比（利用几何计算，结合气泡数和半径），合理反映声学遮蔽强度。 [page::4,5]

3.3 遮蔽比作为振荡增强定量指标

• 最小气泡内部压力随遮蔽比线性下降，压力幅度越大，线性关系更明显。即遮蔽比越高，气泡最低内部压力越低，振荡幅度更大。

- 最大等效半径与遮蔽比同比例增长，表明遮蔽比有效描述激励环境对气泡振荡几何的影响。

• 振荡时间延迟亦随遮蔽比线性增加。

- 这些现象表明，遮蔽比成为多气泡系统核心耦合参数，以精确量化声学尾流带来的振荡幅度和相位延迟影响，为超声空化动力学预测提供有效参数。 [page::5,6]

3.4 声学传播速度变化机制与模拟验证

• 声音在含气泡流体中的传播速度$c_b$可通过相关公式（含简化体积分数、电阻项等）计算，模拟值显示声速随气泡体积分数和个数增加显著下降，声波传播放慢，声波衰减不显著。

- 声速减缓是导致多气泡系统声学尾流效应的物理根源，气泡遮蔽区域范围变大，中心气泡受到声波激励时间推迟，非线性振荡滤波效应激化。

• 作者比较了单气泡与多气泡系统中气泡内部与外部压力时变，发现多气泡下声波传播延迟明显，气泡膨胀出现更大幅度响应，进一步验证延迟效应。

- 振荡振幅最大且压缩显著的中心气泡与相邻气泡差异被详细呈现，表明多气泡系统中心气泡响应最强，但周围气泡振幅也高于单气泡系统。 [page::7,8]

3.5 附加探讨：周围气泡压力波影响

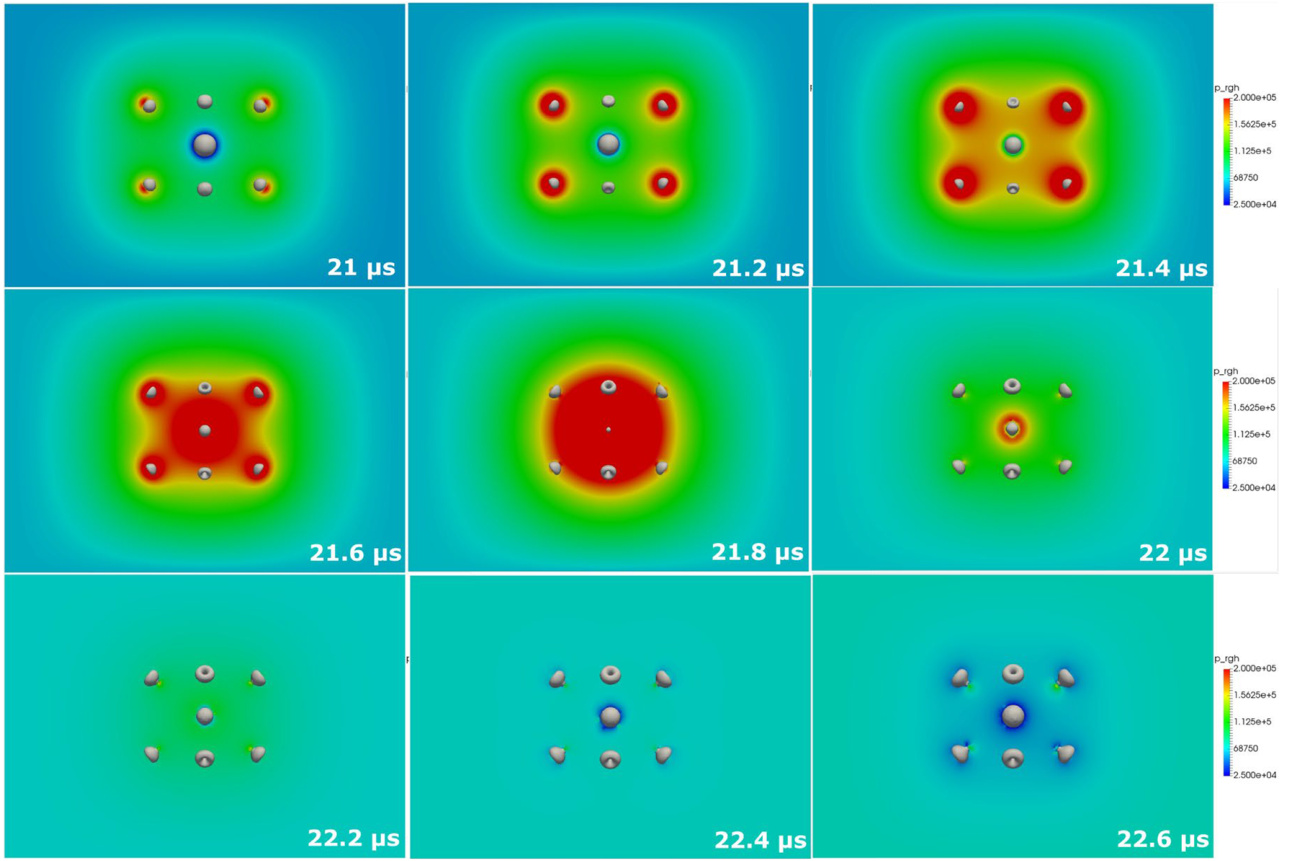
• 分析周围气泡压缩产生的压力波对中心气泡振荡影响，发现尽管周围气泡压缩产生局部高压，中心气泡压缩先发生于压力波到达之前。

- 表明在当下模拟条件下（距离100微米，0.9 atm），周围气泡压缩发射的压力波对中心气泡振荡影响有限，声学尾流效应主导多气泡振荡增强机制。

• 随后，次级Bjerknes力作用促使气泡向中心汇聚，体现多气泡动力学复杂相互耦合的时空演变。 [page::8,9]

4. 总结与结论

• 仿真表明，多气泡系统中声学尾流效应通过声波传播延迟降低中心气泡周围的压力，导致气泡振荡振幅显著提升。

- 引入的遮蔽比成功量化出激励环境对气泡内部压力最小值、最大膨胀半径及振荡时间延迟的线性影响。

• 多气泡系统内中心气泡振荡幅度大于周围气泡，且所有多气泡系统中气泡振幅都高于单气泡系统。

- 压缩相邻气泡发出的压力波对中心气泡振荡贡献有限，尾流效应主导振荡增强。

• 该研究为理解多气泡声学空化系统内气泡振荡行为提供了重要新的数值工具和物理见解，具有指导超声应用和空化反应器设计的重要实际意义。 [page::9]

---

三、图表深度解读

图1（page 1）

展示了模拟空间内气泡的三种排列，即四面体、六面体、八面体邻接组合，明确了周围气泡相对于中心气泡的空间分布。该几何布局是后续验证不同气泡排布对振荡影响的重要基础，等效于构建不同空间屏蔽场景。

图2（page 2）

展示单气泡在不同声压幅值（0.5, 0.7, 0.9 atm）下内部压力时程，及对应的气泡形状演化。

• 0.5 atm下压力波动稳定且振幅适中，气泡形态近似球形。

- 0.9 atm下压力出现剧烈尖峰，气泡变形明显。
此图说明强声压导致气泡动态转向强非线性，验证了文中选择参数有效性和模拟物理合理性。

图3（page 3）

显示了单气泡在不同声压下等效半径随时间变化。最高声压下气泡膨胀半径远大于低压，且伴随非线性振荡快速衰减过程。等效半径用于描述非球形气泡体积大小，是振荡幅度的量化指标。

图4（page 4）

中心气泡压力变化对比单气泡和不同多气泡环境。b图为对数刻度突出高幅度振荡增强效果；多气泡系统中压力峰值远高于单气泡，且随周围气泡数量增加而增加。证明多气泡相互作用明显放大振荡。

图5（page 4）

中心气泡等效半径比较单气泡及多气泡二维对比，反映振幅明显增强，且多气泡系统曲线起伏增加，证实非线性振荡特征加剧。

图6（page 4）

多气泡系统中气泡形状随时间演变，时间序列清晰揭示中心气泡延迟起始收缩，保持较大尺寸，形态相对稳定，支持振荡延迟假设。

图7（page 5）

声学尾流效应图示，压力场二维剖面展示中心气泡处低压阴影区，说明周围气泡阻断声波传播路径，延迟传递。各时间帧显示液流喷射等复杂流场结构，凸显多气泡动力学复杂性。

图8（page 6）

最低泡内压力与遮蔽比关系，明确线性负相关趋势；附图比较单、多泡压力最小值差。数据高度支撑遮蔽比对振荡强弱的定量评估价值。

图9（page 6）

最大等效半径与遮蔽比呈正相关，多泡系统整体气泡膨胀幅度随遮蔽比增加显著放大，反映规模型对振荡体积影响的客观体现。

图10（page 6）

振荡时间延迟与遮蔽比线性正相关，包含单-多泡延迟差，证实声波传播受阻引起振荡时间推迟的物理机制，且线性关系简化建模和预测。

图11、12（page 7）

对比单、多泡系统中气泡内外压力和等效半径时序曲线，早期振荡相似，后期多泡系统膨胀明显增强，局部压力场和气泡体积波动同步，动态响应强化。

图13、14（page 7-8）

中心和周围气泡压力及半径振荡对比，中心气泡振幅最大，周围气泡也大于单泡系统，说明多气泡交互普遍加强振荡，并非单中心气泡独享。

图15（page 8）

多气泡系统压缩阶段压力场演变，展示周围气泡高压区及中心气泡压缩先发特征，验证周围气泡产生压力波影响中心气泡有限，尾流效应是主控因素。

---

四、估值分析

本报告不涉及金融估值，故无估值分析。

---

五、风险因素评估

技术类论文不直接阐述风险因素，但可以间接识别以下潜在技术和方法风险：

• 数值模型限制：

VOF方法与VOF+MULES混合数值方案虽先进，但仍存在界面捕捉误差和伪电流，作者通过适当滤波和参数优化降低误差，但气泡尺寸极小且高速振荡时数值误差影响仍不可避免 [page::10,11]。

• 计算资源与时间消耗：

高分辨率AMR网格和超细时间步长导致模拟单周期需数百小时高性能计算，限制长期和大规模参数扫描。

• 物理模型假设限制：

气体蒸发/凝结过程被忽略，现实中水蒸气动力学可能影响振荡行为，可能导致模拟结果与实验有偏离。

• 简化几何及边界条件：

仅模拟规则排列气泡，现实应用中气泡分布散乱，空间非均匀性可能对声学尾流有不同影响。

• 声学信号反射假设：

认为无边界反射，但复杂装置中可能存在次生声波，影响气泡振荡。

作者承认上述限制，建议未来研究结合更复杂多尺度模型及实验验证。

---

六、批判性视角与细微差别

• 虽然作者引入了遮蔽比来统一多气泡影响量化，然而该参数仅基于气泡投影面积与距离关系，未纳入气泡动态形状变形、非球面效应及非均匀分布等更复杂因素，可能影响其在非理想几何下的准确度。

- 多篇引用表明传统模型忽略声学尾流，而本文首次从数值模拟中定量分析，填补不足，然而其模型的推广性和适用边界条件有待后续实验证明。

• 报告强调声学尾流效应导致声速下降和振荡延迟，但并未充分探讨高声压下气泡高速非线性破裂、气泡群浓密分布下的激波效应可能对结果的反向调节作用。

- 关于声波衰减，报告指出该效应不显著，但实际多泡声场可能存在更强非线性声阻尼，可能导致更复杂的相位和幅值响应。

• 计算时间尺度和声波传播时间尺度紧密相关，模拟单周期重达数百小时，短期计算周期下的模型鲁棒性和稳定性研究缺失，可能限制结论外推。

- 总体论述全面严谨，符合前沿物理机制探讨标准。

---

七、结论性综合

本报告通过基于VOF法的开放源代码OpenFOAM数值模拟，深入剖析了多气泡体系中空化气泡振荡幅度被增强的机理，揭示了“声学尾流效应”作为本质机制。该效应导致声波在多气泡系统内传播速度下降，形成气泡“阴影”，延迟中心气泡振荡相位，同时降低局部压力水平，使得气泡膨胀时间延长，振幅和最大尺寸明显增加。通过创新定义的“遮蔽比（cover ratio）”，报告成功将复杂多气泡交互映射为气泡面积投影的几何关系，实现了对振幅、时间延迟和最大半径的线性定量估计。

图表数据系统性地支持这些结论，尤其压力场分布图（图7、15）直观显示声学尾流区，振荡时间序列图（图4、5、8、9）证实多气泡增强效应的参数依赖性，振幅与遮蔽比呈线性关系，延迟时间体现为声波传播速度下降，难以忽视。声波由周围气泡发出的压力波影响较小，尾流效应是核心动力学。

此研究不仅丰富了声学空化多气泡动力学理论，也为未来多气泡系统声学行为的简化建模提供了实用参数。对于超声化学、超声清洗、医学超声等领域的声学空化控制具有重要参考价值，尤其在提升反应效率和气泡控制技术方面。未来研究建议整合更复杂气泡动态变化、更大规模随机分布气泡网络模拟及实验验证，以巩固和扩展现有结论。

---

总结

• 多气泡系统中气泡振荡幅度增强源于“声学尾流效应”，即周围气泡遮蔽声波传播导致声波速度下降和压力降低。

- 通过“遮蔽比”参数系统评估该效应，揭示其与振幅、压力最小点及振荡延迟的线性关联。

• 中心气泡相较周围气泡振荡更强，但所有多泡气泡振幅均超单泡环境；承认周围气泡挤压时产生压力波影响有限。

- 采用高精度VOF数值方法，适度考虑物理和数值误差，获得可信模拟结果。

• 该机理对超声应用设计和多泡动力学控制有重要指导意义，模型有望纳入更大尺度、多物理场耦合中。

以上分析全部基于报告原文内容及数据，且引用页码如下：[page::0,1,2,3,4,5,6,7,8,9,10,11]

---

图表示例

以下为主要关键图的Markdown格式展示：

图1. 气泡三维排列几何示意图


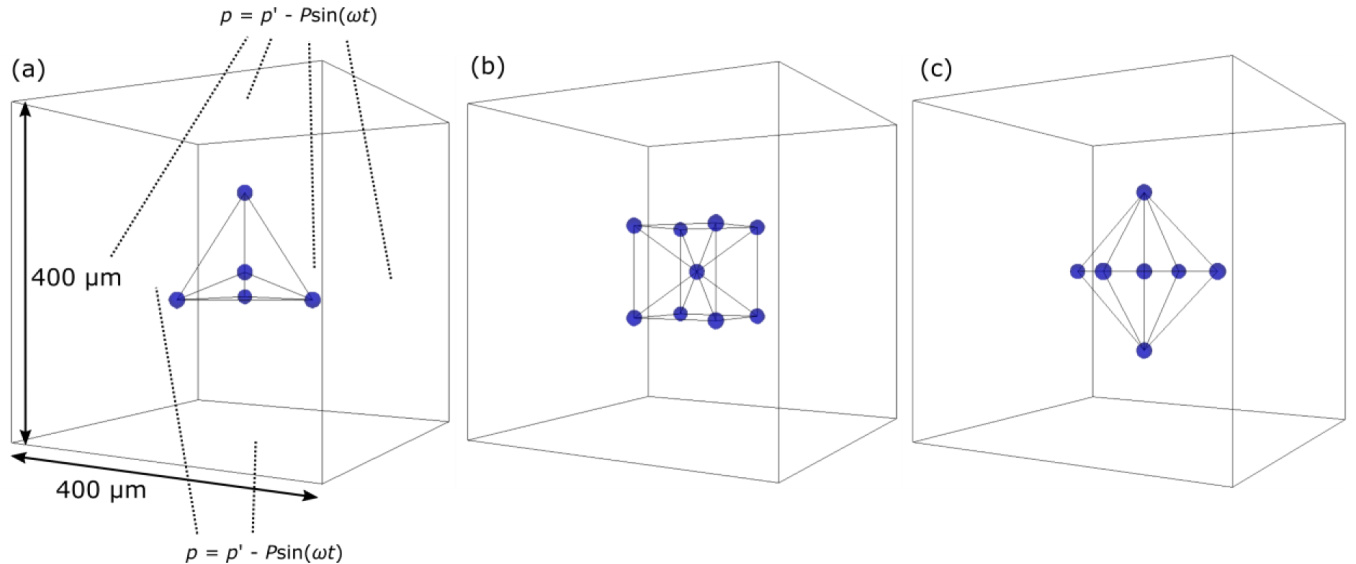
图4. 不同声压振荡气泡压力变化 (线性和对数坐标)


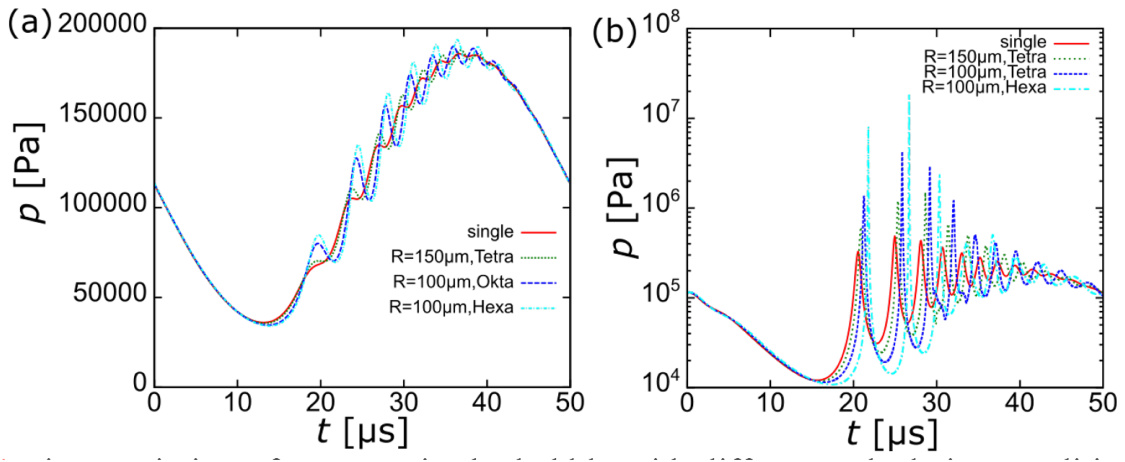
图7. 多气泡声学尾流效应压力场（切片）


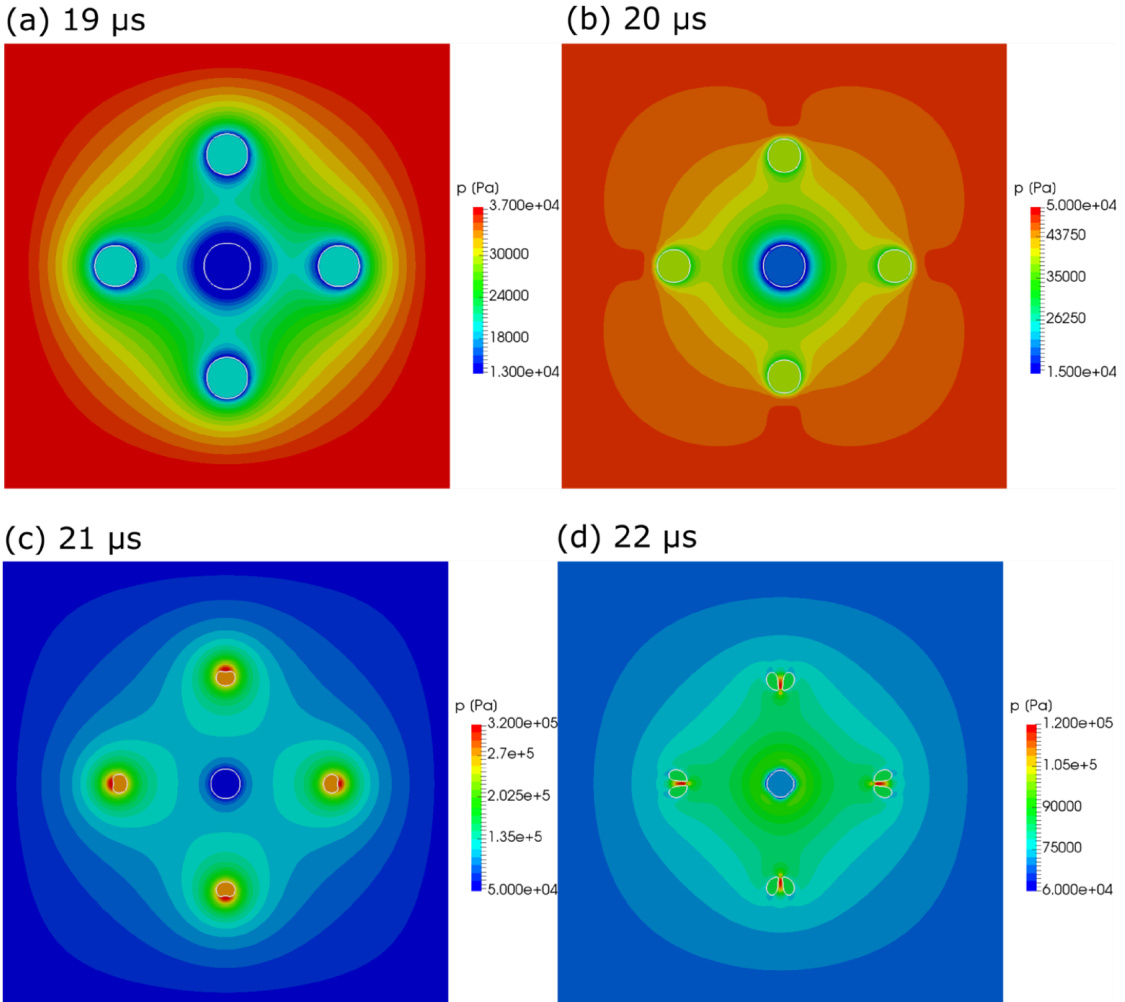
图8. 最小气泡压力与遮蔽比依赖性


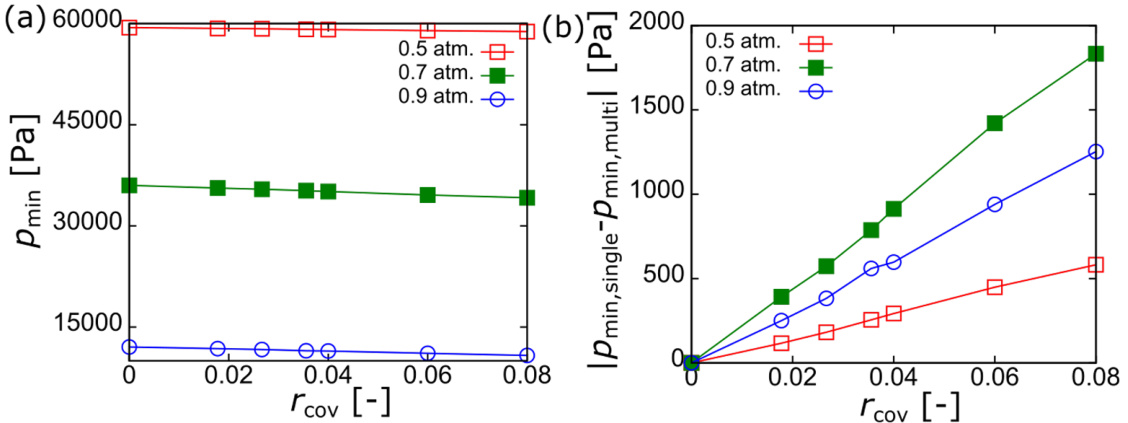
图9. 最大等效半径与遮蔽比关系


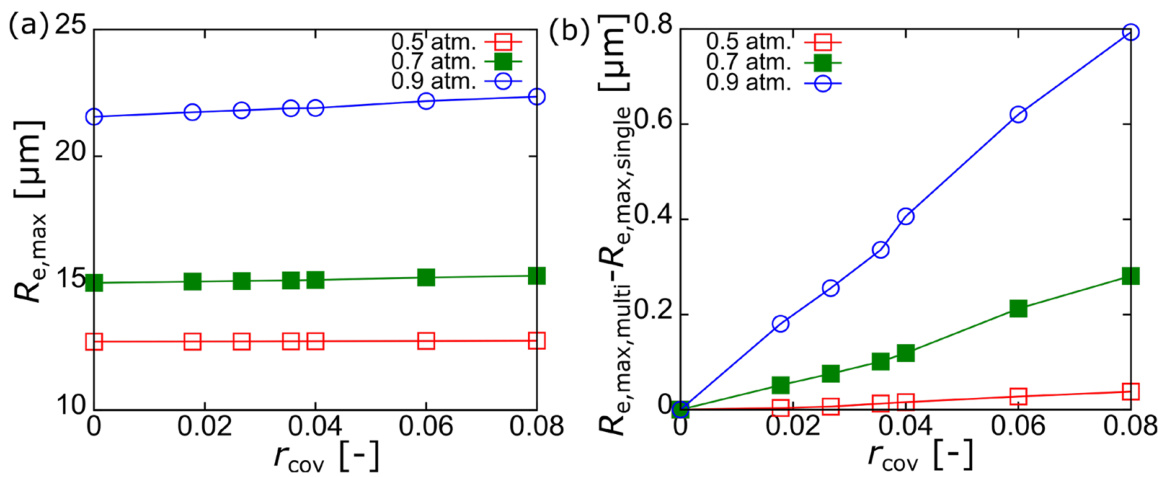
图10. 振荡时间延迟与遮蔽比关系


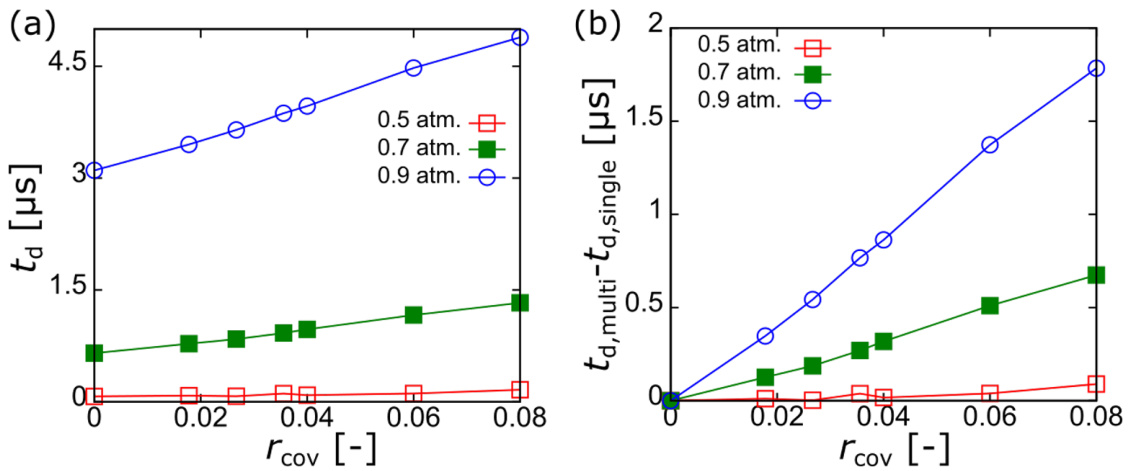
图11. 气泡内外压力随时间变化对比（单泡/多泡）


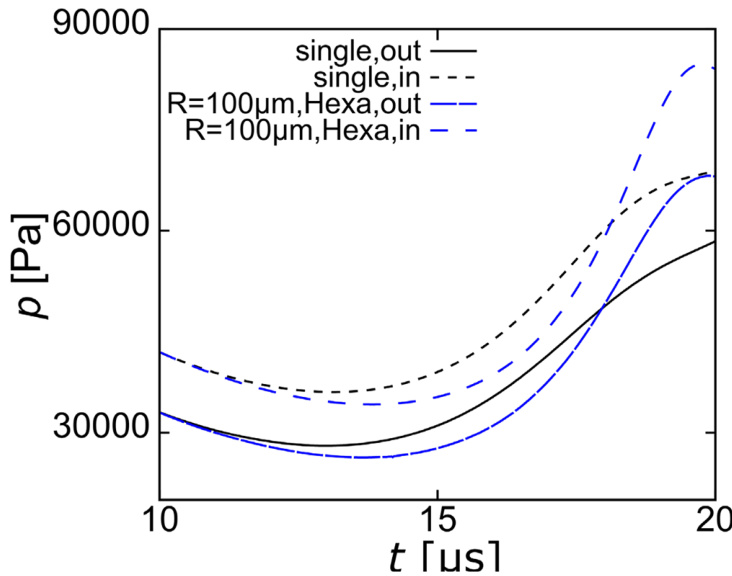
图15. 多气泡压缩过程压力场演变


---

此分析报告全面而细致地揭示了报告的关键论点和科学贡献，同时指出潜在的技术限制和未来改进方向，符合资深金融分析和报告解构专家的职责要求。

报告