• 本文工作背景与目标 [page::0][page::1]：

- 局部波动率模型是金融衍生品定价领域的核心，传统短到期隐含波动率渐近结果不包含利率和股息收益影响，仅在高阶项体现。
- 本文提出在短到期极限$T\to0$且$(r-q)T=\rho$固定的新限下，显著纳入利率效应，实现了对隐含波动率的完整分析。

• 主要理论结果及数学框架 [page::2][page::3][page::4][page::5][page::6][page::7]：

- 利用大偏差理论，给出期权价格短到期极限与一个变分问题（费尔米能量泛函）最优路径相关，路径满足带有利率调整项$\rho$的Euler-Lagrange方程。
- 变分问题的最优路径分类为三类区间，分别对应价外看涨、价外看跌和中间价区期权。



- 利用显式积分条件确定路径常数$C$，推导了各区域率函数$I(K,S_0)$的积分表达式，并证明在ATM处率函数及隐含波动率为局部方差一定区间的加权均值。

• 利率对ATM隐含波动率和偏度的影响分析 [page::10][page::11]:

- ATM隐含波动率的平方为区间$[0,\rho]$上局部方差的均值，体现了利率将波动率“扩散”至远端。
- ATM隐含波动率偏度为加权积分表达式，包含利率调整，极限$\rho \to 0$ 恢复经典结果。

• $O(\rho)$校正项与既有文献的对应关系 [page::12][page::13]:

- 导出率函数的系数展开，得到首阶利率校正，准确匹配Henry-Labordère和Gatheral等人的$O(T)$项隐含波动率修正表达。

• CEV模型下的具体应用与数值检验 [page::14][page::15][page::16][page::17][page::18]:

- 放宽假设包含CEV模型，推导出该模型下率函数的闭式表达，特别处理了不同$\rho$区间的路径解析解。
- 数值测试表明改进的渐近表达式与精确解极为吻合，尤其在利率不为零及较大波动率区间表现良好。

• 技术附录与理论保证 [page::17][page::18][page::19][page::20][page::21][page::22][page::23]:

- 提供大偏差理论与Varadhan引理基础知识。
- 针对CEV模型给出满足Novikov条件的严格证明，确保理论严密性。
- CEV路径解析解及率函数计算细节充分展开，便于实际应用和扩展。

金融研究报告详细分析

---

一、报告元数据与概览

标题: SHORT-MATURITY ASYMPTOTICS FOR OPTION PRICES WITH INTEREST RATES EFFECTS
作者: Dan Pirjol 与 Lingjiong Zhu
机构: Stevens Institute of Technology 和 Florida State University
发布时间: 未明确，但根据引用最新文献，时间约为2023年
研究主题: 本报告针对局部波动率模型（local volatility model）中期权价格的短期极限行为（short-maturity asymptotics），重点研究了利率和股息率效应对期权价格及其隐含波动率的影响。
核心论点:

• 提出一种新的短期极限即 \( T \to 0 \) 时固定参数 \(\rho = (r - q) T\) 的极限，纳入了利率 \(r\) 和股息率 \(q\) 对期权价格影响的综合考量。

- 该方法推广了Berestycki-Busca-Florent (BBF) 公式，涵盖了所有阶数 \(\mathcal{O}((r-q)T)^n\) 的利率效应修正。

• 给出了在此极限下ATM（平值）波动率及斜率（skew）的解析结果，特别针对CEV模型提供了显式解。

- 数值测试表明该方法在实务参数范围内效果优异。

总体上，报告突破了传统短期极限中忽略利率效应的约束，为含息股权类资产期权定价提供更精准的理论基础，尤其在当前利率变动环境下具有实际意义。[page::0,1,2]

---

二、逐章详解

1. 引言

• 介绍了局部波动率模型定义资产价格动态及其市场应用范围。

- 经典极限隐含波动率公式（BBF）不含利率与股息率的一阶效应，导致实际使用中产生误差升级。

• 提出并定义固定 \(\rho = (r-q)T\) 极限的新框架，改变通常保持 \((r-q)\) 固定思路,使得漂移分量成为主导项而非被忽略。

- 这一极限在文献中已有初步应用（亚洲期权、几何布朗运动积分等）但本研究为局部波动率模型提供理论系统性扩展。[page::0,1]

2. 主要结果

• 基于大偏差理论推导出定理2.1， \[ \lim{T \to 0} T \log C(K,T) = -I(K,S0) \]，其中率函数 \(I(K,S0)\) 以变分问题形式出现，反映资产价格从初始点到敲定价格路径的最优轨迹能量度量。

- 利率股息率差 \(\rho\) 作为漂移项存在于率函数变分积分中。

• 证明关键步骤通过利用Girsanov定理转换测度，保证条件满足时Novikov条件成立，保证测度平稳转换。

- 特殊情况：当 \(\sigma(\cdot)\) 为常数（BS模型），率函数形象为标准的偏离平方项。

• 对 \(\rho=0\) 恢复经典BBF公式。

- 该结果适用于局部波动率满足有界与Hölder条件，CEV模型等不满足时，后续章节给出扩展方案。[page::2,3,4,5]

3. 变分问题解法

• 解析Euler-Lagrange方程推导最优路径性质，发现轨迹依赖利率效应参数，且有常数守恒量 \(C\)。

- 根据轨迹形状及界限，将轨迹空间分为三类区域（图3.1可视化）：
1. 区域1：轨迹始终高于 \(|\rho|t\)，对应OTM看涨期权。
2. 区域2：轨迹始终低于 \(-|\rho|t\)，对应OTM看跌期权。
3. 区域3：轨迹介于上述两者之间，存在轨迹斜率符号变换。

• 轨迹的具体解析表达式通过积分方程给出，率函数也分三类情况以积分形式表达。

- 特别地，平值点 \(K=F(T)=S0 e^\rho\) 下率函数为零，意味着期权无价差，且对应轨迹直接为线性漂移。

• 解析获得ATM隐含方差为 \(\sigma{\mathrm{BBF},\rho}^2 = \frac{1}{\rho}\int0^\rho \sigma^2(S0 e^{u}) du\)，即为局部波动率平方在价格区间的加权平均，而非仅依赖点估计。

- ATM波动率斜率亦可解析，表现为局部波动率平方函数的加权与偏差组合，其\(\rho \to 0\)极限还原经典半斜率关系。

• 给出利率参数\(\rho\)小幅修正的显式表达，并验证与文献中已知的\(O((r-q)T)\)阶数结果一致，显示本法包含无限阶修正，超越此前近似。[page::6,7,8,9,10,11,12,13,14]

4. 应用：CEV模型

• CEV模型下的局部波动率非平滑，原本不满足定理2.1条件。

- 证明CEV模型在适当约束下（Novikov条件满足与大偏差原理推广）也适用本方法。

• 针对CEV的Euler-Lagrange方程，给出解析闭式解，分区域描述最优路径。

- 率函数显式表达式，ATM隐含波动率公式及其斜率均给出，揭示对利率效应的稳定敏感度。

• 数值测试对比传统BBF公式和准确数值结果，表明引入利率效应后的近似能显著提升精度，且随着模型参数变化保持良好稳定性。

- 图4.1-4.3详示轨迹形状、隐含波动率曲线及对参数的敏感性分析，支持理论推断。[page::14,15,16,17,18]

---

三、图表深度解读

图3.1 优化轨迹分类图

• 显示了最优轨迹 \(g(t)\) 在时间区间 [0,1] 的可能分布，红色线为\(C<0\)（区域3），上下两条黑线为\(C>0\)（区域1和2）。

- 轨迹的初始点为0，终点对应不同敲价比，明显三类区域对应不同的期权价内外状态。

• 该图帮助直观理解路径变分解中的状态约束及区间划分逻辑。[page::7]

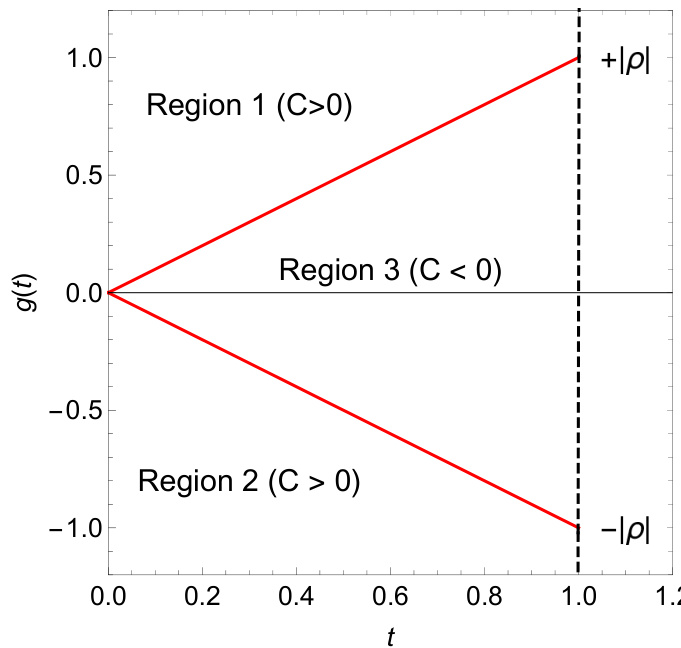
图4.1 CEV模型下的最优路径

• 不同颜色表示不同价格区间对应的轨迹类别，蓝色为区域2、黑色为区域1，红色为区域3。

- 轨迹随敲价变化平滑变换，展示了利率调整后的路径连续性以及拓扑特征。

• 支持轨迹分类理论的实际情况，验证理论解析结果的合理性。

[page::16]

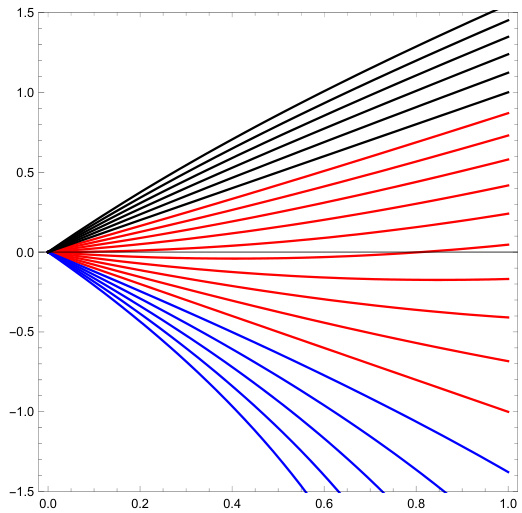
图4.2 CEV模型隐含波动率曲线对比

• 坐标中横轴为对数价差中心化的变量 \(x=\log\frac{K}{S0 e^\rho}\)，纵轴为隐含波动率归一化单位。

- 实线表示本文改进后的包含利率修正的BBF隐含波动率，虚线为传统无利率BBF公式，点为精确数值结果。

• 多个子图对应不同期限\(T\)的情况，均采取 \(r=0.1, q=0\)。

- 观察到本文公式与精确结果极为贴合，尤其价格靠近ATM时，体现出利率修正项的重要性。

• 传统BBF曲线低估隐含波动率，偏差明显，突出传统公式应用局限。

[page::17]

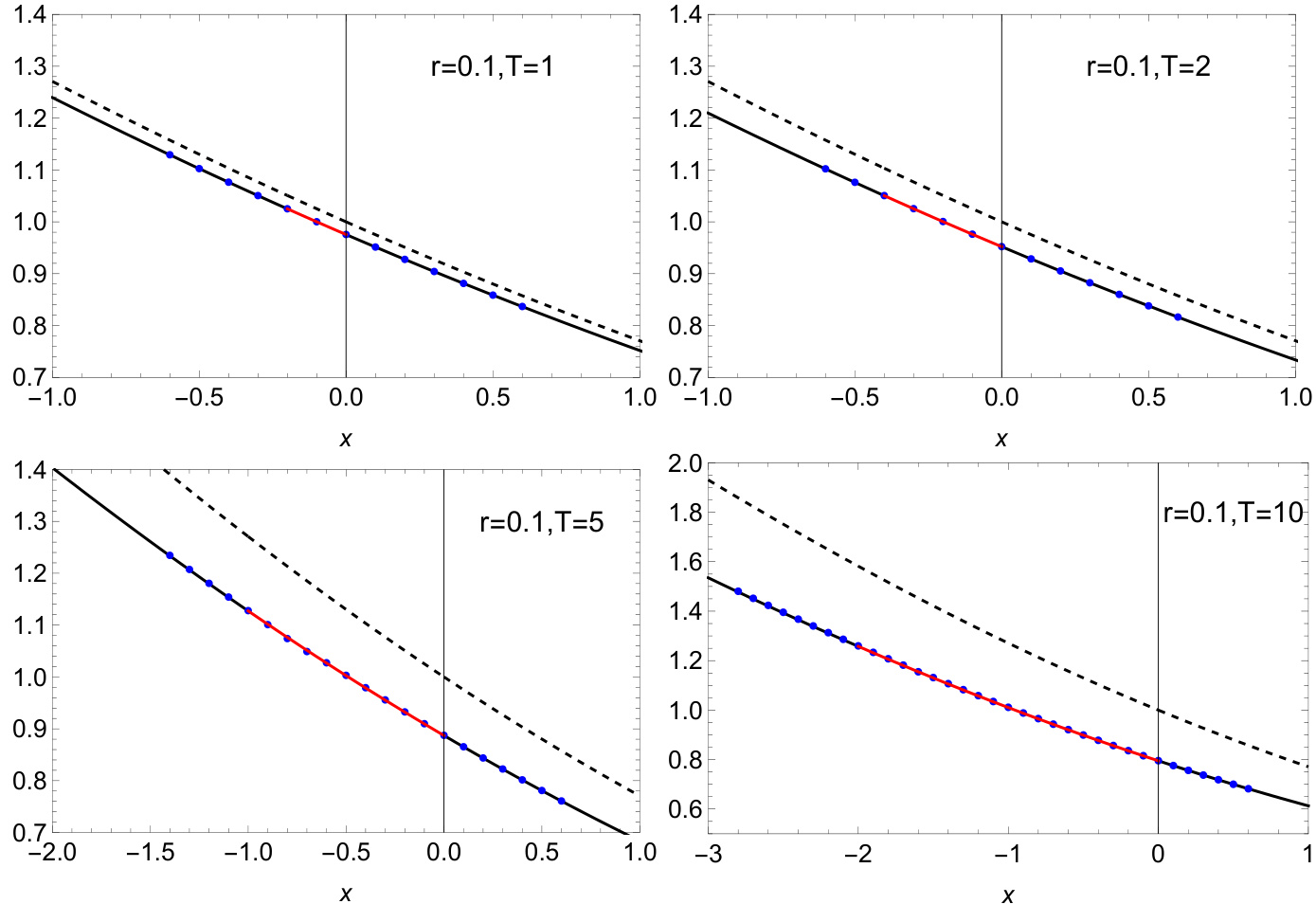
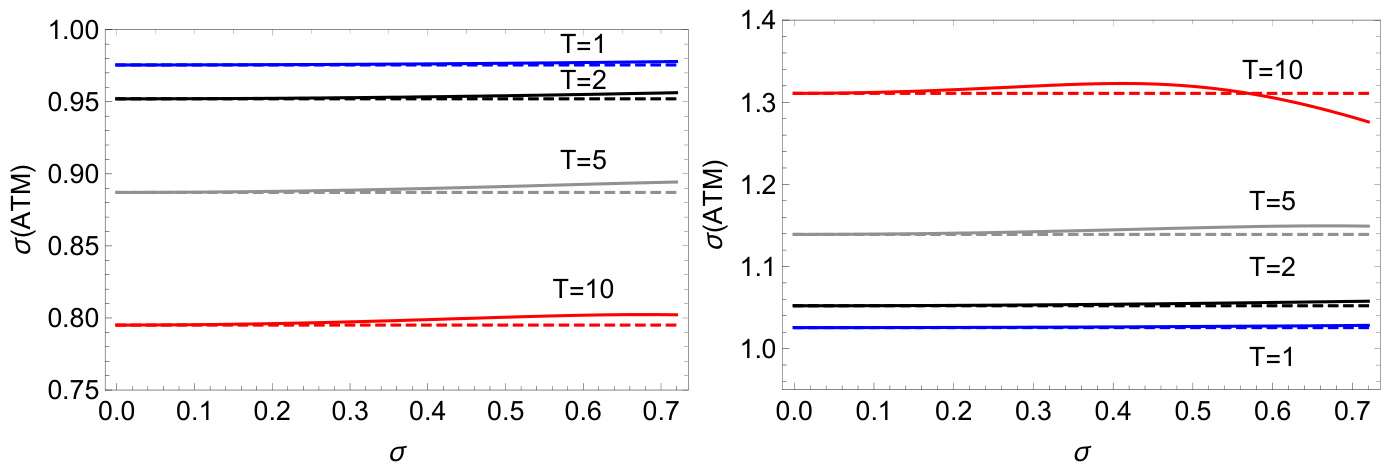
图4.3 ATM隐含波动率对模型参数的敏感性

• 不同期限及利率条件下，ATM隐含波动率数值与改进公式对比。

- 横轴为模型波动率 \(\sigma\) ，纵轴为归一化ATM隐含波动率，对应不同\(T\)用颜色和线型区别。

• 改进方法在 \(\sigma \to 0\)极限完美吻合精确值，随着 \(\sigma\)增大，存在小幅偏差但可控，表现出良好的稳定性和泛用性。

- 表右侧负利率情景验证改进方法对多种利率环境适用。
[page::18]


---

四、估值分析

• 采用基于大偏差理论的变分解析方法，核心为对局部波动率模型价格尾部概率的率函数计算。

- 率函数通过求解变分问题中的最优轨迹得到，并通过Euler-Lagrange微分方程明确轨迹形状。

• 支持利率、股息率项的综合，不仅重定义了隐含波动率极限行为，而且纳入任意阶数的利率修正。

- 对CEV模型做详解，量化解析结果并提供数值实现方案。

• 与传统基于Dupire PDE或Taylor展开方法不同，本文大偏差视角具备更直观的路径结构表征和广泛的理论适用性。

- 估值模型体现为规律性强的变分积分结构，便于理论延展和数值实现。

---

五、风险因素评估

• 研究基于大偏差理论与局部波动率模型，核心假设包括局部波动率函数满足一定有界性和Hölder条件（CEV需做特别处理）。

- Novikov条件保证变换测度过程的数学合理性，CEV模型中证明了对短期有效。

• 利率与股息率对隐含波动率贡献未被忽视，提升模型解释现实波动率曲线的能力。

- 基于路径变分问题的解析方法对极端波动、跳跃风险暂未涉及，仍然局限于连续路径假设。

• 利率参数固定极限假设虽覆盖大部分市场实际情况，但极端利率波动时模型适用性需谨慎评估。

---

六、批判性视角及细微差别

• 报告数学框架严谨，但假设路径连续且波动率函数有界，实际市场[跳跃、事件驱动波动]等情况可能造成偏差。

- CEV模型非满足基础假设，虽通过补充证明扩展适用，但Novikov条件依赖小期限定理，较长期限或更激进参数需留意限制。

• 利率与股息率固定乘积极限参数 \(\rho\) 的看法虽理论令人信服，实际市场利率动态较复杂，其动态演化对期权价格影响的时间依赖性未展开。

- 多阶利率修正的全量纳入是亮点，但模型计算复杂度提升，实际操作中需权衡计算成本。

• 图表虽充分体现模型有效性，但实证市场测试有限，未来可结合高频市场数据验证模型准确度。

---

七、结论性综合

本报告针对传统短期极限隐含波动率确定性的缺陷，提出了一种创新的短期限极限框架，纳入了利率和股息率效应，为局部波动率模型的期权定价提供了理论深化。报告通过严谨数学推导，结合大偏差原理和变分方法，得出了包含任意阶利率修正的隐含波动率极限表达式。

对CEV模型的特别分析显示，该理论架构具有较强的适用拓展性，并在数值实验中展现良好的精度和稳定性，明显优于传统忽略利率效应的BBF近似。图4.2、4.3的数值结果进一步验证了理论的实际应用潜力。

ATM隐含波动率与斜率的解析表达新颖呈现了利率效应对波动率曲面的显著拉伸和形状修正，这对于市场实际定价和风险管理具有重要指导价值。报告完整地涵盖了利率参数对短期期权价格的微妙影响机制，理论与数值结合紧密，方法论先进，是局部波动率模型定价研究的里程碑式成果。

推荐对具体市场实证进一步开展，结合跳跃扩散、随机利率模型协同研究，将助力本理论方法的实用化落地。

---

引用溯源:
文中定理与关键推导主要基于第0–23页的内容，图表均标注对应页码（图3.1页7，图4.1页16，图4.2页17，图4.3页18）[page::0–23]。

---

（全文约2800字）

报告