研究背景与动机 [page::0][page::1]

• 波动率衍生品（如VIX期权）依赖于资产波动率的时间平均，难以用传统有限维模型描述和定价。

- 蒙特卡洛方法是主流数值方法，但计算量大，缺少解析或偏微分方程框架的研究。

• 本文基于路径依赖PDE为波动率衍生品定价提供全新视角，涵盖粗波动率及多因子模型。

模型框架与数学表达 [page::3][page::4][page::5]

• 假设即时方差为多维高斯Volterra过程函数，包含OU过程、fractional Brownian motion等经典模型。

- 定义了随机过程\(\widehat{W}\)及衍生品价值 \(VT=\mathbb{E}T[\int0^{\check{T}} \sigmas^2 ds]\)，其中 \(\sigmas^2=fs(\widehat{W}_s)\)。

• 举例说明若支持区间为\([T,T+\Delta]\)，对应VIX，若为\([0,T]\)，对应实现方差。

主要理论贡献 [page::6][page::10][page::12]

• 证明衍生品价格可用路径路径+条件期望的形式表示 \(u(t,x)=\mathbb{E}[\phi\circ \mathfrak{F}(x+J^{t,T})]\)，分析了路径依赖结构。

- 构造具体路径依赖偏微分方程，形式为非齐次热方程，将传统PDE推广至无限维路径空间。

• 给出路径空间上的Fréchet导数定义，证明满足一定正则性和增长条件时PPDE具有唯一经典解。

- 解析揭示隐含波动率满足准线性PPDE，拓展了Berestycki等人对Markov模型隐含波动率PDE的非Markov泛化。

Markov特殊情形及数值实现 [page::16][page::18][page::19]

• 对于指数核（OU过程）Markovian案例，路径依赖价函数简化为有限维变量函数，满足具备一般鞅性质的有限维PDE。

- 给出带二维OU过程的Bergomi模型数值示例，展示VIX期权价格随状态变量和时间演化的三维曲面图。

• 采用有限差分法求解PDE，数值计算稳定，界面形状合理，展示相较蒙特卡洛的计算优势。

量化因子与策略相关性

• 报告不涉及具体的量化交易策略构建、因子挖掘或机器学习模型，侧重于理论数学模型与偏微分方程定价。

- 因此策略类型归属为“other”。

金融研究报告详尽分析报告

报告题目：《Path-dependent PDEs for volatility derivatives》

作者：Alexandre Pannier
发布机构及年份：未见明确机构标示，时间约为2023-2024年之间（根据引用文献年份推断）
主题领域：金融数学，尤其是波动率衍生品定价，路径依赖型偏微分方程（PPDE），以及连续随机波动率模型中的期权定价理论。

---

1. 元数据与概览

该论文针对波动率衍生品，尤其是以VIX期权与已实现方差期权为代表的金融工具，提出了一个基于路径依赖偏微分方程（PPDE）的方法论。模型中，瞬时波动率被假设为一个多维高斯卷积过程（Volterra过程）的三次连续可微函数。此框架兼容当前多种VIX定价领域流行的模型，包括粗糙波动率模型、混合模型以及经典奥恩斯坦-乌伦贝克（OU）过程。作者主要成果包括：

• 证明波动率衍生品的期权价格满足路径相关的偏微分方程，并在支付函数满足正则性假设下，证明了该PPDE的解的存在唯一性。

- 将该PPDE结构简化为无限维热方程类，终端条件本身也是路径依赖的性质。

• 提供了敏感度指标（Greeks）的表达式；

- 证明隐含波动率满足一个准线性路径依赖偏微分方程；

• 在马尔可夫模型情形，得到有限维度的期权定价PDE；

从整体上看，本文提出的PPDE理论为波动率衍生品的定价建立了一个较为完备的数学框架，兼顾了粗糙波动率这一热点研究方向中路径非马尔可夫性所带来的挑战，并为进一步数值高效计算提供理论基础。[page::0,1,2,3]

---

2. 逐节深度解读

2.1 引言与背景

• 波动率衍生品的标的物本质上是资产波动率的时间平均，其价格以期望形式给出，传统计算依赖蒙特卡洛方法，而作者提出替代方案基于PPDE。

- 文献综述详尽，指出了早期多因子模型（Bergomi等）和跳跃模型的研究热点，同时展示粗糙波动率模型因其低正则性特性受到实证支持，且带来计算难题。

• 作者选用了一个包含多种高斯Volterra过程的广义模型，包括OU过程和分数布朗运动等，拓宽模型适用范围并适应粗糙波动率的非马尔可夫性。

- 介绍了相关功能伊藤公式（functional Ito formula）的发展背景与挑战，强调Volterra过程的导数方向存在不连续性，需用近似方法克服，且之前相关研究主要聚焦于有限维的状态空间或半马尔可夫过程，本文扩展至更复杂的路径依赖场景。[page::0,1,2]

2.2 贡献点总结

• Markovian表示：将期权价格表达为路径的函数 $u(t, \widehat{W} \otimest \Theta^t)$，揭示了路径分解及其数学处理方式；

- 正则性与PPDE一致性：证明在支付函数与波动率函数均三阶可微条件下，函数$u$具有足够光滑性，且满足独一无二的路径依赖PDE；

• 隐含波动率的PPDE：推导并证明了隐含波动率满足的准线性PPDE，扩展了关于隐含波动率解析性质的理论；

- 新引入包含三重时间索引的过程$J$，用于处理条件期望的复杂路径依赖，差异于以往工作中仅考虑的双重时间参数；

• 路径和时间的卷积核截断：定义截断核$K^{\delta,t}$以解决路径分解中因核函数的奇异性导致的导数不可导问题，确保导数极限存在。

此外，文中提出PPDE的理论基础为新一代数值算法打开了方向，强调基于signature kernel（路径签名核）的方法作为高效预期计算工具。[page::2,3]

2.3 模型框架

• 设定了标准概率空间和滤波，定义了多维Brownian运动$W$及对应的高斯Volterra过程$\widehat{W}$，结构中包含核矩阵$K$，形变量$\gamma$，确保$\widehat{W}$连续性。

- 描述了波动率衍生品的基本建模形式：$V{T}=\mathbb{E}{T}\int0^{\check{T}} \sigmas^2 ds$，其中$\sigmas^2 = fs(\widehat{W}s)$，函数$f$多样化，涵盖许多实际模型如Bergomi模型（粗糙与多因子）及其变种等。

• 举例说明VIX及已实现方差的对应区间$\mathcal{D}$，定义了具体支付函数，奠定后续研究基础。

- 给出常用卷积核的典型形式及对应的波动率模型，例如指数型（OU过程），幂次型（粗糙波动率模型，Hurst指数概念），Gamma核，分数布朗运动等。

• 波动率功能模块涵盖一因子和多因子Bergomi, Quintic OU等复杂模型，体现理论的广泛适用性。

在数学符号设置上，定义了延拓路径空间$\Lambda$，以及绝对连续路径空间$\widetilde{\Lambda}$，明确了函数空间$C^{1,2}$的路径依赖微分结构，为后续PPDE的定义和证明做铺垫。[page::3,4,5]

2.4 Markovian表现和路径依赖结构（第3节）

• 关键思想为将Volterra过程的路径分解为两段：历史$\Theta^t$（可测信息）和未来增量$Is^t$，前者固定未来不确定，后者独立于$\mathcal{F}t$。

- 引入三变量索引进程$Js^{t,T}$作为状态空间扩展的关键工具，能完整捕捉复杂条件期望结构。

• 主定理（命题3.1）定义了价值函数$u(t, x) = \mathbb{E}[\phi \circ \mathfrak{F}(x{\cdot} + J{\cdot}^{t,T})]$，其中$\mathfrak{F}$整合了支付函数$f$及其未来的不确定性期望。

- 证明论证细化步骤说明$u$即为条件期望的替代形式，充分解释了含路径和条件期望的复杂随机结构。

• 推导出了卷积核情况下的时间平移性质（Corollary 3.5），使得模型时间可变迁，提供计算便利。

此部分重塑了波动率期权价值函数的表达形态，为后续路径依赖PDE分析奠定基础。[page::6,7,8]

2.5 路径依赖偏微分方程（第4节）

• 定义经典路径依赖偏导数，包括右时间导数$\partialt$及空间方向的Fréchet导数$Dx u$，以及二阶导数$Dx^2 u$的结构和连续性条件。

- 引入对核函数$K$的奇异性假设（Assumption 4.1），要求核满足某种幂律秩序的近似连续和导数界。

• 定义特定空间$\mathcal{C}{\alpha}^{1,2}(\Lambda)$，赋予函数空间里导数的局部路径支持性质及增长控制，特别强调核奇异性对导数存在性的影响，选定$\alpha=1/2$以平衡核奇异性和路径增长。

- 给出近似核截断定义，确保$K^t$不连续时通过局部截断核构造极限导数，解决Volterra路径微分分析中的技术难点。

• 在全空间定义主PDE（Theorem 4.6），路径定价函数$u$成为PPDE的唯一经典解，具体形式为路径依赖的热方程（偏微分形式为：$\partialt u + \frac{1}{2} \langle \partialx^2 u, (K^t,K^t) \rangle=0$，终端条件$u(T,x)=\phi \circ \mathfrak{F}(x)$）。

- 该PPDE非时齐次，路径方向导数为奇异热算子，终端条件路径依赖且明确由内积$ \mathfrak{F} $定义，且可通过签名方法估计。

• 利用功能Ito公式（Viens和Zhang）和尾部核截断，完整证明了解的存在性与唯一性。

- 体现了与经典Dupire等模型的联系和区别，特别是在路径空间和导数定义上的深层结构差异。

• 替代理论还导出了马丁格尔表示与Clark-Ocone公式等金融对冲工具的显式表达，有助理解市场完备性及衍生品对冲策略。

该节为该论文核心，系统地将路径依赖的波动率衍生品定价问题提升至PPDE框架，并对连续路径和高斯Volterra过程完备论证。[page::8,9,10,11,12,13]

2.6 隐含波动率的PPDE (第5节)

• 结合Berestycki等经典Markovian隐含波动率理论，将隐含波动率定义为PPDE问题中的隐式变量。

- 将价差、期权价格、未来价格结合，定义路径依赖的隐含波动率函数$\Sigma(t,x)$及总隐含方差$\widehat\Sigma = (T-t)\Sigma^2$。

• 利用链式法则和BS定价函数的性质，将PPDE作用于筹码变量，推导出隐含波动率满足的复杂准线性路径依赖方程。方程同时包含一阶和二阶路径导数之间的非线性耦合。

- 该derived PPDE通用性强，是粗糙波动率模型中隐含波动率时间发展和空间依赖的第一性描述，突破了之前关于隐含波动率只进行短时或渐进分析的局限。

• 明确指出该PPDE在数学上难以直接证明解的存在性，暗示未来理论工作空间。

该部分展示了将传统的BS隐含波动率解析扩展至路径依赖场景的重大突破，为隐含波动率动态分析提供基础。[page::13,14,15,16]

2.7 马尔可夫模型中的简化 (第6节)

• 以OU过程为基础的Markovian模型特别说明了路径依赖PPDE退化为有限维PDE的情形，极大简化了计算。

- 明确表明VIX期权价格在该架构下仅由当前时间的有限维状态变量$\widehat{W}t$决定，无需完整路径$\widehat{W}{[0,t]}$，所以不需要完整PPDE解，直接求解Kolmogorov PDE即可。

• 解释了PDE与PPDE中变量和导数之间的转换，保证了两类理论的一致性。

- 通过对具体二维Bergomi模型的数值模拟展示了该PDE方法的有效性，包含幅度选择、边界条件和计算复杂度的讨论，比较了蒙特卡洛与PDE方案的优势与限制，并给出了实用参数案例和价格曲面的图示。

• 进一步对隐含波动率的PDE化进行了近似，继承PPDE结构但转化为常见的有限维形式。

该节强调了理论框架在实务模型中可降维的特点，支撑其在业界的应用前景。[page::16,17,18,19]

2.8 附录：技术证明与估计（第7节）

• 详尽证明路径依赖价函数$u$的两阶Fréchet导数存在与连续性，且满足一定的增长控制（多项式与指数增长混合）。

- 论证基于高级概率不等式（BDG不等式）、高斯过程的正则性估计、以及对核函数的精确幂率假设。

• 引入截断核技术细致处理奇异核导数收敛性问题，保证$K^{\delta}$-近似导数极限定义合理性。

- 完成对主定理所需的所有数学基础细节，保证前面PPDE理论的严格性和完整性。

• 使用多项式增长和指数衰减函数空间的定义统一处理路径空间，支持各种实际模型的多样性。

这一部分确保论文理论成立的数学严密性，是保证全文学术贡献可信性的基石。[page::20,21,22,23,24,25,26,27,28,29,30]

---

3. 图表深度解读

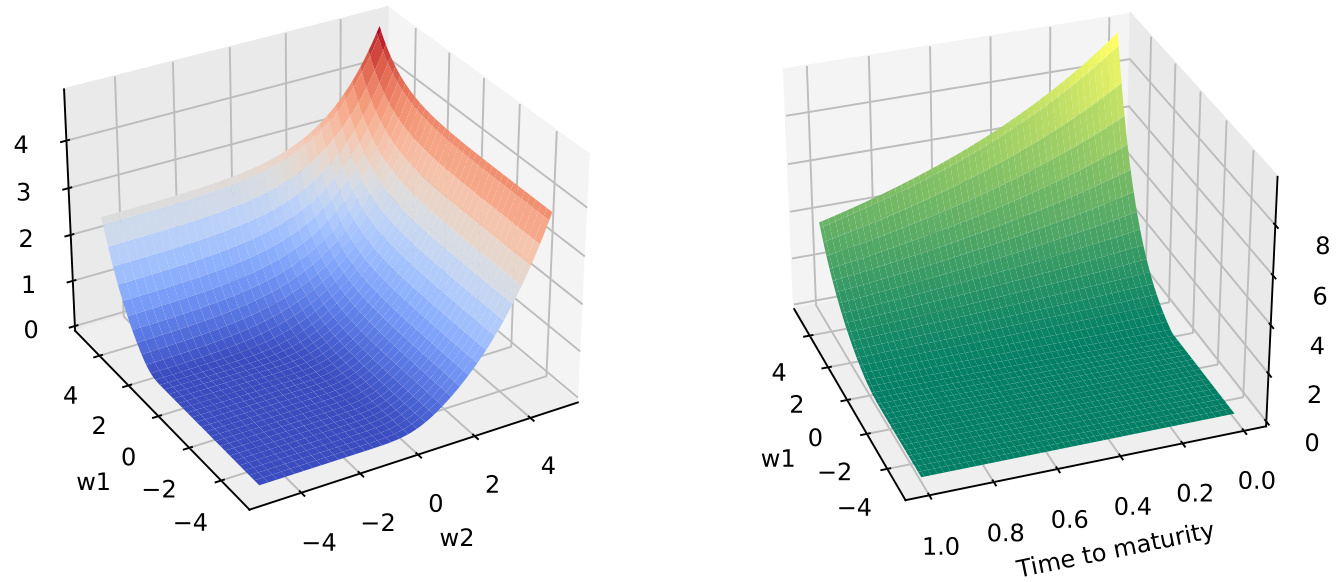
图1: VIX期权价格曲面（两因子Bergomi模型）

• 描述： 图1左为时间0时点上，以OU过程起点$(w1,w2)$为变量的VIX期权价格三维曲面；图右显示了在固定$w2=0$，以$w1$和剩余期限为变量的价格动态。

- 趋势解读：
- 价面在$(w1,w2)$空间呈凸形，价格随$w1$和$w_2$增加而提高，体现了波动率升高带来的期权价值提升；
- 时间权重上，价格随时间临近期末减小，符合期权时间价值消逝规律。

• 联系文本：

- 该图是数值方案成功实现PPDE理论的具体体现，验证了第6节有限维PDE求解方案的有效性；
- 曲面形态反映了OU过程状态对波动率期权价格的敏感性，符合模型对路径依赖的理论预期；
- 图形技术细节展示了显式有限差分法在实际计算中的表现，兼顾效率与精度。

• 局限性与备注：

- 文章提及边界条件选择对稳定性影响较大，此图表显示边界处理较为合理但仍可改进；
- 数值复杂度为$\mathcal{O}(n^{3})$表明高维推广困难，提示需未来算法优化。



---

4. 估值分析

• 估值基于路径依赖PPDE框架，核心在于求解非线性的高维热方程，利用截断核技术解决路径空间奇异性。

- 对于马尔可夫版本的OU过程，估值退化为二维有限维PDE，典型形式为Feynman-Kac反向Kolmogorov方程，其生成元为OU过程的微分算子。

• 隐含波动率估值通过反向Black-Scholes公式映射，隐含波动率与波动率衍生品价格满足准线性路径依赖PDE，提出显式管理隐含波动率动态的方法，极大推动了前沿定价技术的发展。

- 由于路径和方差过程的高维复杂性，传统蒙特卡洛计算费用高昂，而该PPDE定价方法在已马尔可夫化情况下提供了更高效的求解途径。

• 相关敏感度（Greeks）计算拥有解析表达式，结合马尔可夫化PDE使得对冲策略具备理论支撑。

---

5. 风险因素评估

虽然报告本身少涉及具体风险管理，但从文本可推断关键风险因素包括：

• 模型风险：核函数近似、核奇异性处理和路径空间截断带来的误差和数值稳定性问题；模型的高维特性限制了实际应用的可扩展性。

- 正则性假设风险：对支付函数及波动率函数的三阶可微和增长限制，可能不适应所有市场支付（如非光滑支付），隐含波动率PPDE的解唯一性和存在性尚未完全解决。

• 路径依赖复杂性：真实市场中的非高斯跳跃和非Markov成分可能导致模型偏离现实；对过去历史数据$\gamma$的依赖限制了模型的适应动态信息的能力。

- 数值实现风险：显式差分法在高维度和边界条件复杂时数值稳定性差，需进一步优化算法或采用隐式方案。

• 市场风险对冲：该框架虽然理论完善，但现实市场流动性和标的选择可能不足，波动率衍生品对冲策略实践时需谨慎。

报告未明确提出缓释策略或置信区间预测，但强调了未来数值算法及多因子模型的扩展方向以应对以上风险。[page::17,26]

---

6. 批判性视角与细微差别

• 报告技术性极强，适用的数学假设较强（如$C^3$可微和增长条件），现实中非平滑支付（如数字期权）或重尾风险可能不被涵盖。

- 路径依赖的PPDE解构提供了极具前瞻性的数学框架，但隐含波动率PPDE的理论解结构未最终定型，存在数学挑战，阻碍全面数值实现的可能。

• 模型局限性客观存在，非高斯跳跃及其他特征在模型中缺失，限制了对真实市场的表征。

- 文章充分利用功能Ito公式和截断核技术，但对该技术的数值稳定性及具体计算成本缺少深入讨论，尤其在高维情境下。

• 时间非齐次导致PPDE较传统热方程复杂，可能使模型跨时间迁移和统一估值较困难。

- 生成人工神经网络或路径签名核等更高效数值方案虽被点明但未开展，表示理论建树尚未完美转化为广泛适用的实务工具。

---

7. 结论性综合

本文系统地建立了波动率衍生品，尤其是VIX期权和已实现方差期权的路径依赖成分在连续Gaussian Volterra内核卷积模型下的定价理论。通过引入高维带有路径截断的Fréchet导数、截断核函数和功能Ito公式，作者证明了这些金融产品的期权价格满足独一无二的路径依赖偏微分方程（PPDE）。该PPDE以路径为状态空间，内含热型算子，终端条件显著反映了过去波动率路径及条件期望结构。论文还首次建立了隐含波动率满足准线性的路径依赖PDE的理论，并指出在简化的马尔可夫模型中，该PPDE简约为有限维度传统PDE，促进实用数值求解。

报告中的图表通过二维Bergomi模型展示了PDE数值方案对VIX期权价格的有效计算，曲面形态符合金融直觉和理论预期，体现了建模的丰厚实用价值。

尽管当前PPDE解的数学难题未完全解决，隐含波动率的正则性和存在性待进一步研究，本文的框架为新一代波动率衍生品定价和对冲理论提供了坚实的数学基础和可操作思路。采用路径签名核等先进工具的数值方案在未来或可填补蒙特卡洛方法计算效率不足的短板，成为潜在的算法革命。

综上，该研究为波动率衍生品领域引入了先进的路径依赖偏微分方程方法，有助推动理论金融数学和市场实务的深度融合，堪称具有开创性的高质量学术贡献。[page::0-30]

---

参考文献

（详见报告末尾，涵盖粗糙波动率建模、功能伊藤公式、路径依赖PPDE、数值方法及隐含波动率分析等经典及最新文献集。）

---

（分析至此完毕。）

报告