• 论文核心问题为AMM手续费选择如何影响其收益最大化及损失最小化，尤其关注信息化订单流（toxic flow）导致的损失[page::0][page::1]

• 利用随机游走及几何布朗运动（GBM）建模CEX资产价格，证明对称阈值下套利“命中时间”随阈值平方增长，不对称阈值带漂移时线性增长[page::3][page::4][page::5][page::6][page::7][page::8]

• AMM模型采用常数乘积函数模型（CFMM），交易中存在三种价格定义，且价格受到交易非线性影响，套利策略假设CEX流动性无限且套利最优[page::9][page::10][page::11]

- 成功套利的条件为套利收益正，阈值由手续费$f$决定，存在最优套利量$\Delta FL^{opt}$和最优手续费$f^{opt} \approx \sqrt{\alpha}-1$，手续费调节可限制套利造成的AMM损失至三分之一以下[page::11][page::12][page::13]

• 模拟研究显示，静态手续费过低导致费收取不足，过高会抑制套利频率，费率约为价格波动率3倍时收益较优；无漂移时收益恒定，存在套利成功概率随手续费逆比例下降的关系[page::14][page::15][page::17]

• 在有漂移条件下，手续费收益主要来自占多数的代币，收益随手续费线性增加，少数代币收益存在最大值，这与对称与不对称阈值命中时间的理论分析相符[page::18][page::19][page::20]

• 研究结论认为可开发基于市场行情动态调整的异步费率方案，有望提升AMM对有害套利流失的抵抗能力，增加收入[page::21]

深度解析报告：《Role of fee choice in revenue generation of AMMs: A quantitative study》

---

1. 元数据与概览

• 报告标题: Role of fee choice in revenue generation of AMMs: A quantitative study

- 作者: Abe Alexander, Jesse Moestaredjo, Mart Heuvelmans, Lars Fritz

• 所属机构: Utrecht University，Institute for Theoretical Physics and Center for Extreme Matter and Emergent Phenomena

- 发布日期: 2024年6月19日

• 研究主题: 研究自动做市商（AMMs）中费用选择对其收入生成的影响，特别是在去中心化金融（DeFi）中，如何通过优化费用设置来最大化AMM的利润，同时减少因套利引起的损失。

核心论点总结

本文核心在于研究AMM与集中交易所（CEX）之间的套利动态，基于建模套利活动，探讨手续费的选择如何影响AMM的收益最大化。本文指出，动态且方向敏感的手续费设计能够有效缓解套利带来的“有毒交易流”（toxic flow）损失，并提出在不同市场波动及方向偏好下，最优费用设计的理论框架和模拟验证。作者在文中建立了数学模型，结合随机游走、几何布朗运动、之前的文献成果和计算仿真，揭示手续费和套利行为的复杂相互关系，从而为未来设计更优AMM费率和策略提供理论基础和实践建议[page::0,1]。

---

2. 章节详解

2.1 介绍与研究背景

介绍了DeFi中套利的角色——其在价格发现及市场效率维护中不可或缺，但套利同时带来的“有毒订单流”令AMM面临损失。针对蓝筹币对（bluechip pairs）的大量套利操作（占80%以上的交易活动），研究设定假设所有交易均为套利驱动，套利活动在AMM与无限流动性CEX间进行，模型采用几何布朗运动（GBM）模拟CEX价格演化，AMM则以恒定函数市场做市商（CFMM）简化模型处理[page::0,1]。

2.2 相关文献回顾

回顾了AMM基础理论起源和进化，包括Uniswap v3多阶手续费机制、以及动态手续费实现的多个AMM平台和毒性流损失相关研究，突出本文是扩展之前文章[1]的工作，聚焦于基于套利假设的手续费优化[page::3]。

2.3 市场动态建模 — 随机游走与“命中时间”（Hitting Time）

• 讨论一维随机游走模型，定义资产价格变化的离散步骤，表示为资产价格的调整，组成随机过程。

- “命中时间”指从初始价格出发，到价格首次达到某个阈值所需的平均步数。

• 对单侧阈值，命中时间在对称无漂移游走中是无限的，因为存在无穷多路径永不触及阈值（图2 I），但当存在漂移时命中时间变为有限，且与阈值线性关系。

- 对双侧对称阈值时，命中时间为有限且与阈值的平方成比例（$N{\mathrm{hit}} \propto \Delta p^2$），模拟结果（图3）验证了这一结论。

• 若存在漂移（偏向某方向），命中时间变为线性关系（图4）[page::3,4,5,6]。

2.4 价格动态的连续模型 — 几何布朗运动（GBM）

• 介绍GBM的随机微分方程形式及其解析解，强调价格对数服从正态分布且价格保持正值，适用于建模CEX价格波动。

- 该模型用于摩托套利活动中的价格发现机制模拟[page::7,9]。

2.5 AMM的模型设定与套利周期

• AMM模型为恒定乘积公式（CFMM）：$xA \times xB = L^2$，$L$为流动性。

- 讨论了三种价格：现货价格$ps$, 交易时实际交易价格$p{\mathrm{eff}}$，以及交易后的新现货价格$ps^{\prime}$。涉及价格影响因素及非线性定价关系，详见针对一次交换的数学推导。

• 套利过程：套利者利用AMM与CEX价格差异（用$\alpha = p{CEX}/ps$衡量），通过闪电贷借入代币B，兑换成代币A后在CEX卖出获利。

- 交易利润$PB$表达式考虑手续费$f,f{fl}$和交易成本$TXN$，并引入最优闪电贷大小$\Delta FL^{opt}$，推导必要套利条件$\alpha > \alpha{min} = \frac{1}{1-f}$，最优套利时AMM价格接近但未完全等于CEX价格，价格对齐到$ ps' = p{CEX}(1-f)$，直观理解为手续费限制套利完全对齐，防止无利可图的后续套利[page::9,10,11,12]。

2.6 手续费优化与收益最大化

• 设手续费$f$和价格差$\alpha$，优化AMM从套利中获取收益$R=\Delta FL^{opt} \cdot f$。

- 对$f$求导优化，得到近似解$f^{opt} \approx \sqrt{\alpha} - 1$，表明手续费需与价格溢价的平方根相关。

• 收益分配上，手续费优化后AMM最多能获得套利收益的2/3，剩余1/3由套利者获利。

- 讨论“最优套利”与“价格完全匹配套利”策略区别，后者套利阈值更高，发生频率低，手续费收益受影响[page::12,13]。

2.7 数值模拟结果

4.1 价格完全匹配策略模拟

• 在无漂移情况下，根据随机游走理论，套利执行频率与手续费$f$平方成反比，费率收入为$f^{2}$，两者结合使总收入基本常数。

- 模拟（图7）显示，当手续费低于每区块波动率时，手续费收入较低；手续费约为波动率3倍时收益最佳，随后过高应收费导致收入回落。

• 频率随手续费$ \propto 1/f^{2} $变化，符合理论预测。

- 含漂移时，收益和频率分别为$f^{2}$和$1/f$，总收入与手续费线性正相关（图8）[page::14,15]。

4.2 最优套利策略模拟

• 在零漂移环境下（图9,10），AMM价格紧随CEX，有时套利步骤会跳过，价格对齐受手续费比例影响。

- 模拟显示今年，小手续费带来更多低额套利尝试，高手续费则产生更少但大额套利。总收益在足够手续费时与手续费呈线性关系（图10）。

• 交易成功概率随着手续费减小，趋势为$1/f$（图11），符合带有非对称阈值的随机游走理论。

- 结论总结：无偏漂移时，手续费选择差异长远看无关紧要，收益稳定；手续费和收益呈线性乘积和倒数关系平衡[page::16,17,18]。

4.3 含漂移情形

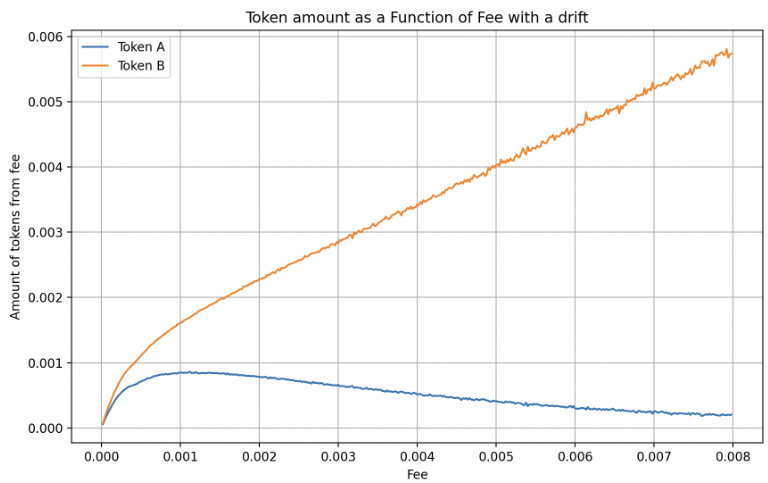
• 当具有方向性漂移时（图12），以溢价方向的手续费产生持续线性增长的手续费收入，无漂移方向手续费收益达到峰值后萎缩（图13）。

- 这是由不同方向套利事件发生概率特性决定：套利概率定值，但单次套利收益随手续费线性增长。

• 在这种情形，AMM应采纳方向敏感、非对称的手续费策略以优化收益[page::18,19,20]。

---

3. 图表深度解读

图1（第2页）

• 内容: 示意AMM与CEX及套利者的互动，AMM价格动态“受制”于CEX价格，CEX价格用几何布朗运动建模，套利者连接两者。

- 解读: 展示了研究核心框架和问题聚焦——是否存在手续费设置能在促进交易前提下最大化AMM收入。

• 作用: 视觉化明确说明套利是连接AMM与CEX的桥梁，手续费选取需兼顾交易活跃和利润优化。

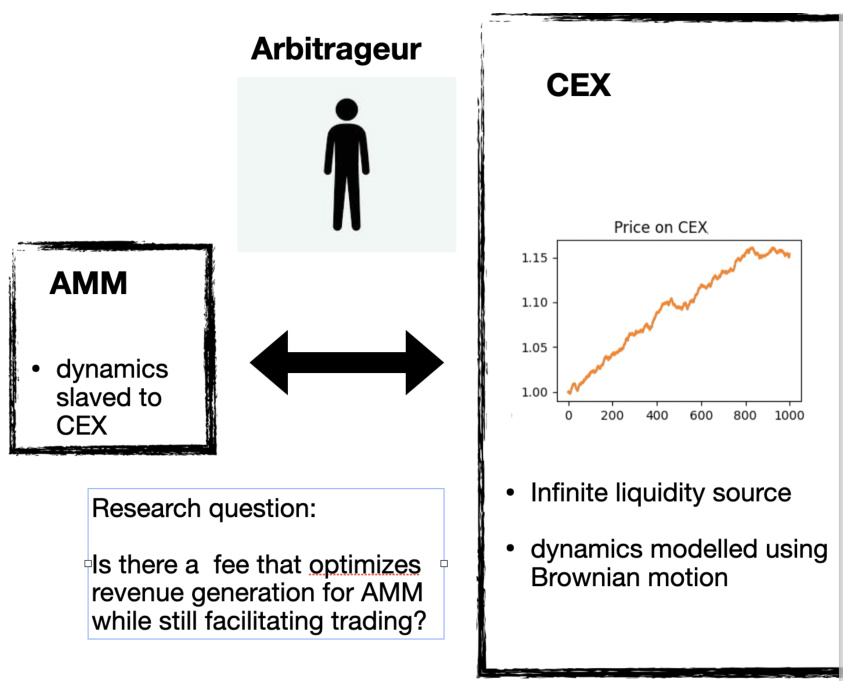
图2（第4页）

• 内容: 两个子图展示随机步进路径对达到单侧阈值和对称双阈值的影响。

- 解读: 图I中单侧阈值下大量路径永不达到阈值，平均“命中时间”无限；图II对称阈限限制路径空间，使得平均命中时间有限。

• 联系: 该统计特征对解释套利事件频率及其与手续费关系尤为关键，特别是非对称阈值情况。

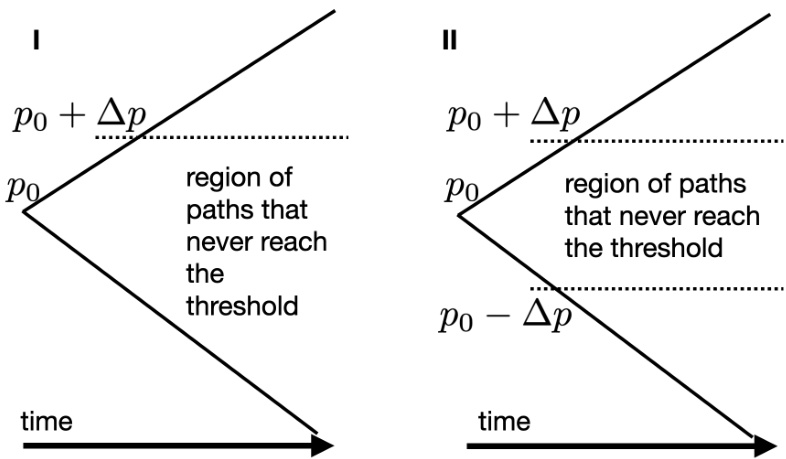
图3和图4（第6页）

• 图3内容: 对称阈值情况下，命中时间$N{\mathrm{hit}}$随着阈值$\Delta p$呈二次方增长。

- 图4内容: 有漂移情况下，命中时间线性增长。

• 解读: 数值模拟验证理论，支持套利成功概率与手续费设置之间的解析关系。

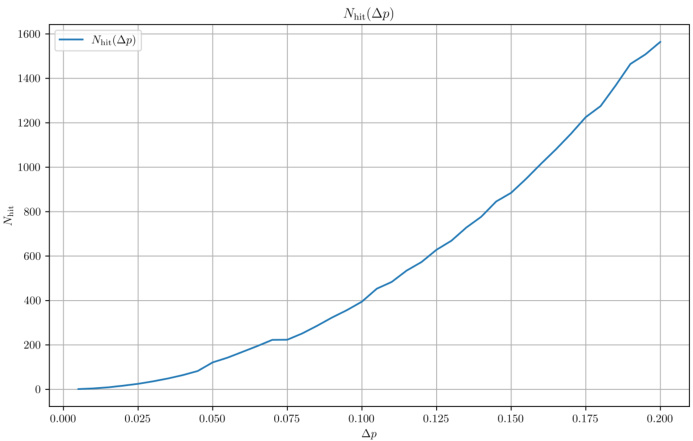
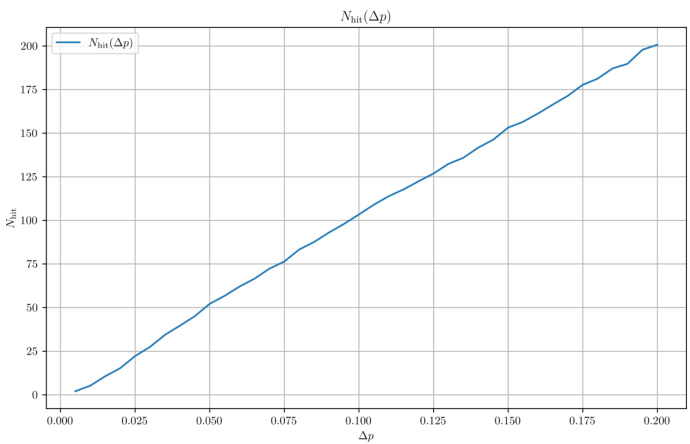
图5和图6（第8页）

• 图5内容: 展示当一个阈值固定，另一个阈值变化时的两种方向偏好情况示意图。

- 图6内容: 数值模拟显示：当漂移方向向着变化阈值时，命中时间线性增长（图6I）；反向则趋于常数（图6II）。

• 解读: 支持非对称阈值模型与套利行为之间的逻辑契合，进一步解释套利成功率的方向依赖。

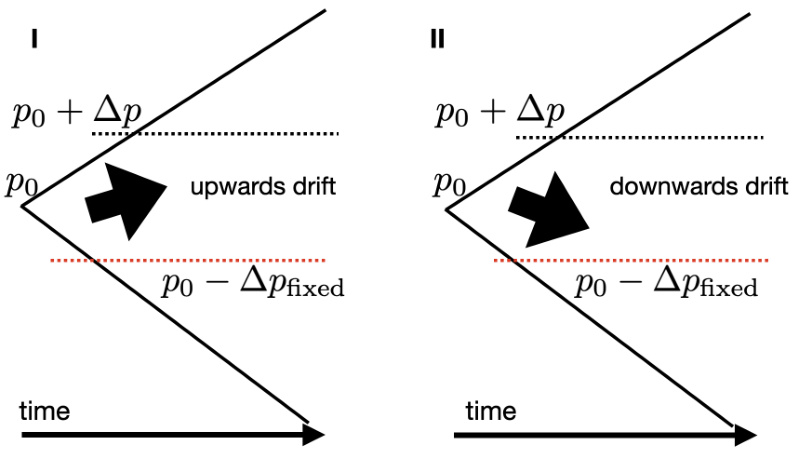
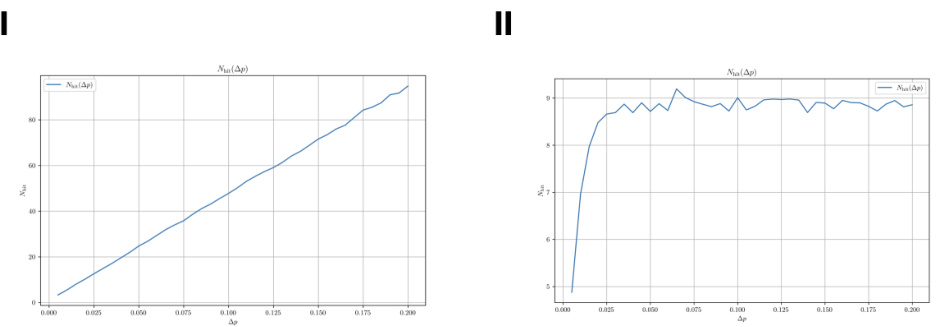
图7和图8（第15页）

• 图7内容: 无漂移情况下，手续费较小时收益低，手续费在约为波动率三倍附近时达到较好收益，手续费过高导致收益下降。

- 图8内容: 有漂移时，手续费收益呈线性增长，无明显饱和。

• 解读: 体现了手续费与收益之间非线性及线性两类动态关系，对手续费设置决策提供定量依据。

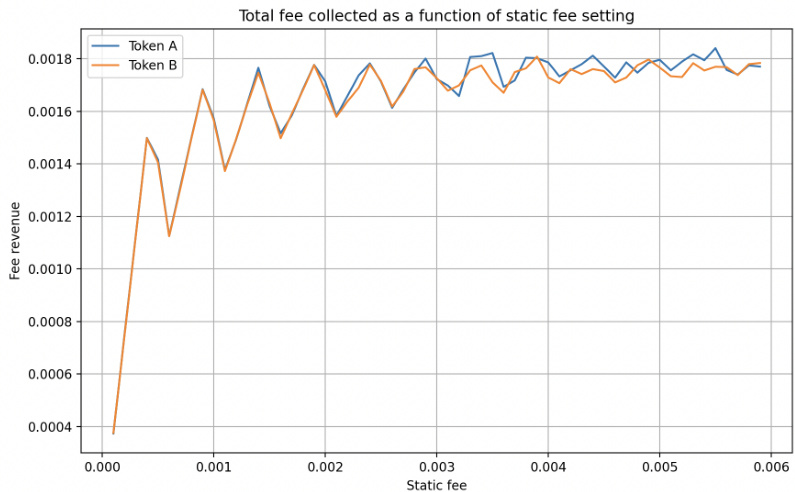
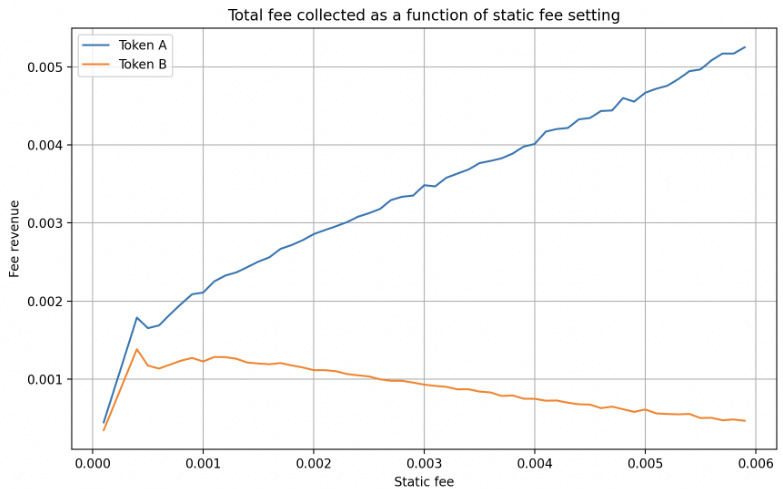
图9（第16页）

• 内容: 30个时间步骤内CEX价格（橙线）与AMM价格（蓝线）变化示意，手续费设为对称0.005。

- 解读: AMM价格基本追随CEX，有时跳过套利，且价格与CEX价格对齐程度受手续费影响，验证价格不完全匹配理论。

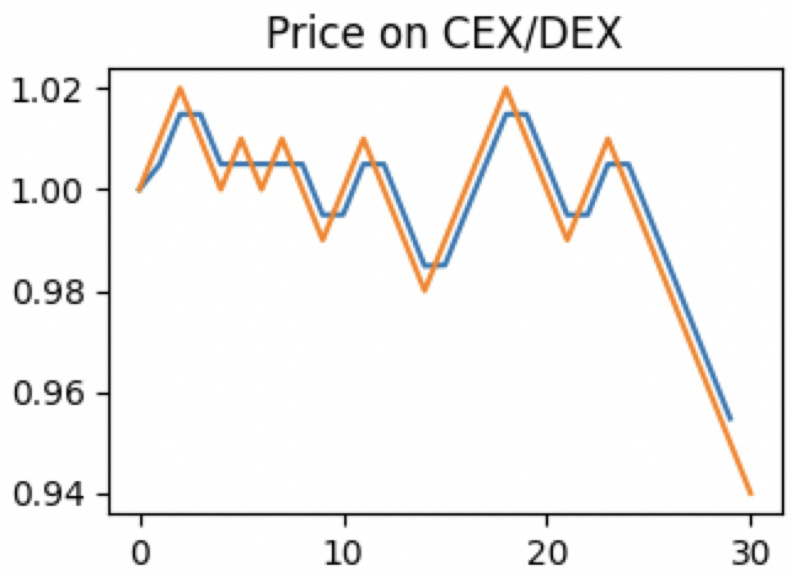
图10和图11（第17-18页）

• 图10内容: 平均手续费收益随静态手续费增长趋势，显示手续费达到一定额度后收益趋于饱和且趋于线性。

- 图11内容: 仲裁事件成功概率随手续费递减，近似$f^{-1}$关系。

• 解读: 两图综合揭示手续费和成功率的互依关系，以及手续费优化的实践限制。

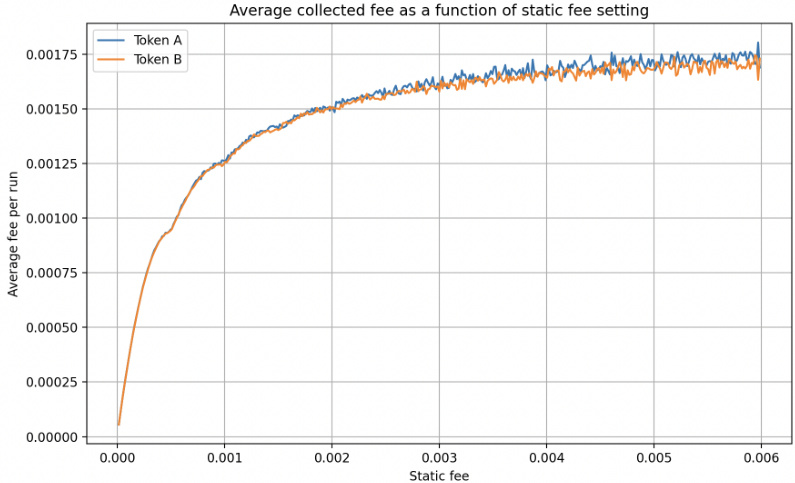
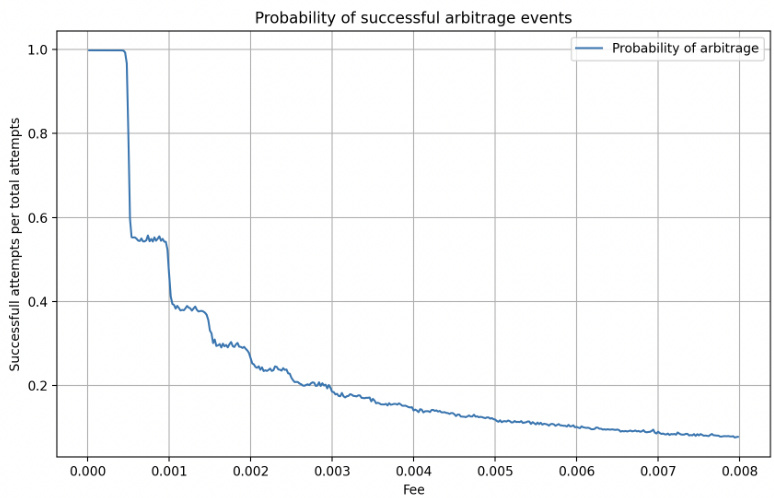
图12和图13（第19-20页）

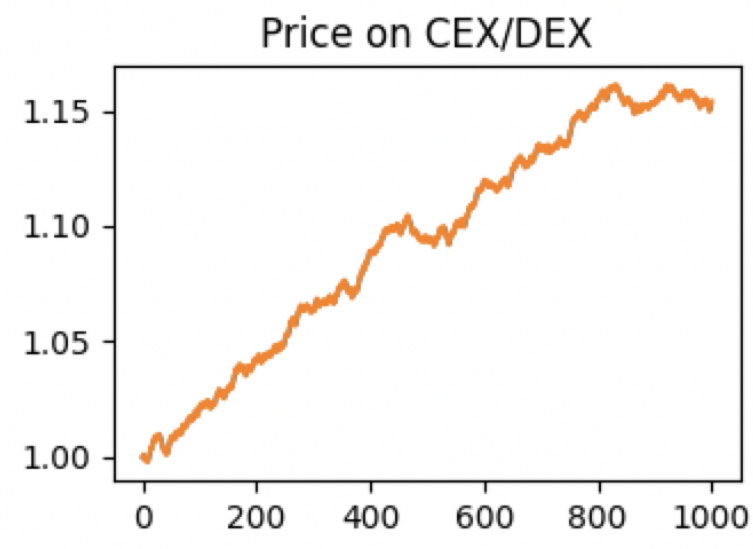
• 图12内容: 含漂移的价格走势示意。

- 图13内容: 含漂移时两代币手续费收益变化，B代币（价格上升方向）收益无饱和且持续增长，A代币先上升后降。

• 解读: 明确手续费收益受漂移方向影响，支持文中提出“动态方向性差异手续费”优化策略。

---

4. 估值分析

本报告虽然非传统意义上的企业估值报告，但基于数学优化模型对AMM“收益”（手续费收入）的估算，实质为对AMM手续费优化的“价值评估”。

• 估值方法基于套利利润最大化和收益分配机制，通过解析套利条件、最优闪电贷额度和手续费收益函数构建收益预期模型。

- 结合随机过程理论（随机游走、GBM）与收益-手续费关系的高阶多项式求解，得出最优手续费$f^{opt} \approx \sqrt{\alpha} - 1$近似表达。

• 此模型旨在寻找费率最大化收益同时防止过度抑制套利导致流动性干涸的平衡点。

- 估值结果依赖于价格波动率$\sigma$、漂移$\mu$、手续费$f$和套利溢价$\alpha$等输入参数的市场动态，基于数学模型和模拟结果验证一致性。

---

5. 风险因素评估

• 模型假设风险: 假设套利全为AMM与无限流动性CEX之间发生，且CEX价格严格按照GBM演化，实际情况中有限流动性、CEX价格突然跳跃或流动性骤降可能影响模型有效性。

- 套利行为简化: 假设套利者完全理性并采用最优策略，在现实中套利行为受信息不对称、网络延迟、手续费变动等多因素干扰。

• 手续费设置动态调整的技术实现难度: 文中提出的方向敏感动态手续费设定需依赖高频行情数据及算法支持，技术复杂度和操作风险较高。

- 合约和智能合约风险: AMM作为智能合约运行，合规漏洞、执行异常等风险尚未讨论。

• 外部市场风险: 监管变化、市场整体波动加剧、极端市场条件等都可能冲击套利频率和AMM收益。

报告并未详细给出风险缓释策略，但呼吁未来考虑“快速调节费率”的算法和实现方案，对风险产生预期管理。

---

6. 批判性视角与细微之处

• 抽象化程度较高: 该报告倾向于数学和模拟建模，复杂市场生态的多维因素（如多策略套利者、非理性交易、链上交易拥堵成本）尚未纳入，可能导致实际应用中效果有限。

- 手续费优化假设独特: 将手续费视为优化变量，且套利动态为唯一驱动力，忽略了非套利交易和流动性供应者的利益，对AMM生态多样性影响未充分考虑。

• 弹性和敏捷性挑战: 动态方向性费率虽具理论优越性，但在现实市场中实施可能面临延迟、算法过拟合及交易策略被利用的隐患。

- 潜在的内部矛盾: 报告中提及不同套利策略对手续费敏感性差异，可能导致实际套利行为复杂化，这一点在模拟中未完全体现。

• 对手续费收入极限的解释较为乐观: 报告指出AMM最多获得套利收益的2/3，但未详细列明该收益分配是否稳健，且在实际市场中受到的其他变量影响未展开。

---

7. 结论性综合

本文系统性地从金融理论与模拟两方面切入，深入剖析了去中心化自动做市商AMM在面临以套利为主交易的大环境下其手续费策略的优化问题。通过精准建模套利对价差触发的随机游走与几何布朗运动机制，报告验证了不同手续费水平对套利频率和AMM收益的显著影响，具体为：

• 零漂移下的价格随机游走，套利命中时间与手续费呈平方关系，套利成功概率与手续费成反比，使得手续费收入在长期呈现稳定且对手续费极值不敏感的“平稳态”。

- 存在漂移（方向性行情）条件下，手续费收入与手续费呈线性正相关，且收取方向性不同的手续费对不同代币的回报表现出明显差异，为设计“动态且非对称手续费策略”提供动力和理论依据。

• 套利收益分配机制表明AMM理论上无法完全消除套利带来的价值损失，但最优手续费设置可限制损失在1/3以内。

- 数值模拟整体验证并丰富了理论推导，模拟数据显示手续费设置应低于或约为价格波动的三倍才能达到收益与交易活跃性的最佳平衡。

• 动态赔率手续费设计为解决toxic flow损失的有希望方案，且报告呼吁开发自动根据市场信息调整手续费的智能算法。

综合而言，作者明确展示了手续费制定环节在AMM收入结构中的核心作用，以随机过程理论为支撑，结合套利的最优行为，为DeFi领域中AMM设计与运营提供了坚实的理论基础和实践参考。

---

（注：文中页码标注对应原文页码，部分引用使用多个页码括号加以表示，如[page::0,1]）

报告