研究背景与动机 [page::0][page::1]

• 股票市场崩盘导致重大经济损失，精确预测极端负收益有助于风险管理。

- 传统GPD模型缺乏对市场状态的动态反映，本文通过将尺度参数建模为协变量的对数线性函数，提升尾部风险预测能力。

数据描述与波动率测度 [page::1][page::2]

• 研究使用Nifty 50指数日度数据（2007-2025年），关注超过-2%、尤其是超过-5%的极端跌幅事件。

- 波动率采用经验波动率和Garman-Klass波动率两种方法，日波动率通过EWMA方法估计并年化，显示两者之间较高相关性。

模型构建与贝叶斯正则化先验比较 [page::2][page::3][page::4][page::5][page::6]

• GPD回归模型中，负收益超过阈值的尺度参数服从对协变量的对数线性回归。

- 对回归系数引入四类先验：Cauchy、Lasso（Laplace）、Ridge（高斯）、Zellner的g先验。

• 采用最大后验（MAP）估计，避免MCMC计算负担，方便模型筛选。

- 模拟研究显示Cauchy先验在预测准确性（RMSE=11.36）、AIC、BIC指标上表现最佳且计算效率最高。

| Metric | Cauchy | Lasso | Ridge | g-prior |
|------------|---------|--------|--------|---------|
| RMSE(y) | 11.36 | 10.37 | 10.65 | 10.43 |
| RMSE(β) | 0.10 | 0.16 | 0.16 | 0.18 |
| RMSE(ξ) | 0.08 | 0.08 | 0.09 | 0.11 |
| AIC | 162.67 | 177.15 | 175.74 | 180.94 |
| BIC | 176.97 | 191.44 | 190.03 | 195.24 |
| 时间(相对) | 1.00 | 175.64 | 155.69 | 2476.86 |

印度市场极端事件实证分析 [page::7][page::8]

| 模型 | RMSE | AIC | BIC |
|------------|-------|---------|---------|
| Cauchy | 1.58 | 298.06 | 322.20 |
| Lasso | 1.80 | 311.57 | 335.71 |
| Ridge | 1.73 | 302.07 | 326.20 |
| g-prior | 1.94 | 308.12 | 332.25 |

• Cauchy先验模型优于其他先验，提供最低的AIC、BIC和RMSE。

- 波动率变量（Nifty、S&P 500、黄金）显著正向影响极端损失的条件期望和崩盘概率。

• 发现明显的全球波动率溢出效应及避险资金流动特征。

- 高波动率下崩盘概率超过60%，极端损失金额剧增。

结论与展望 [page::8]

• 贝叶斯GPD回归有效预测印度市场极端风险，Cauchy先验在正则化中效果最佳。

- 模型同时考虑了本地与全球风险驱动因素，具有较强解释力和预测稳定性。

• 该框架适用于系统性风险监测与压力测试，未来可扩展动态、分层贝叶斯模型。

金融研究报告详尽分析报告

报告元数据与概览

• 报告标题：Predicting Stock Market Crash with Bayesian Generalised Pareto Regression

- 作者：Sourish Das

• 发布机构/时间：未明确披露机构，公开日期为2025年6月19日

- 主题：利用贝叶斯广义帕累托回归（Bayesian Generalised Pareto Regression, 简称GPR）模型来预测印度股市（以Nifty 50指数为代表）的极端下跌或崩盘风险。

• 核心论点：

- 通过建立一个基于GPD（广义帕累托分布）的回归框架，使得尾部风险（scale参数）能够根据市场和全球动态波动（使用协变量表达）而变化，实现对极端负收益的动态预测。
- 评估四种贝叶斯正则化先验：Cauchy先验、Lasso先验（拉普拉斯分布）、Ridge先验（高斯分布）以及Zellner的g先验，结果显示Cauchy先验在准确性和模型简洁性间表现最优。
- 实证部分以印度Nifty 50指数极端负收益（跌幅超过5%）为对象，选用来自Nifty 50、标普500及黄金的波动率作为协变量捕捉内外风险因素。发现尾部风险随波动率显著提升，且标普500和黄金波动率分别体现了全球溢出效应和避险需求。
- 本模型优于传统极值理论（EVT）模型，因为其实时融入了动态的金融指标，适合实践、监管和政策制定者用于系统性风险监控和压力测试。[page::0,1,7,8]

逐章节深度解读

1. 引言

本节强调股市崩盘的严重经济后果和预测极端风险的重要性，引用文献展示COVID-19股市崩盘对预期和波动的影响与结构变化。指出传统极值理论（EVT）利用GPD对极端事件建模效果良好，但忽略协变量导致难以反映市场状况变化。文献中已有部分工作尝试结合协变量，如Liu [2011]和Rai et al. [2022]，但需更加灵活且参量不宜过多导致不可识别。作者动机是以GPD回归模型对规模参数进行协变量建模[page::0,1]。

2. 数据洞察

数据涵盖印度Nifty 50自2007年9月至2025年6月的日收盘价及对数收益率。数据显示多个超过5%每日跌幅，尤以2008金融危机和COVID-19期间明显。定义-2%为显著冲击阈值，-5%为巨大亏损阈值。通过EWMA（指数加权移动平均）计算日波动率，具体采用k=21交易日窗口和0.9的平滑系数，以增强对近期市场波动的敏感性。引入Garman-Klass波动率估计方法，结合高低开收价计算，降低估计方差，捕捉盘内风险特征。

通过散点图及对数尺度图分析实证波动率与Garman-Klass波动率相关系数达0.71，说明两种方法在捕捉波动率上表现一致且相辅相成。此外，结合标普500和黄金波动率来体现全球市场风险传递和避险需求的影响，展示了极端负收益和不同维度波动性的相关关系[page::1,2,3]。

3. 方法论

本节具体建立广义帕累托分布GPD的回归模型，定义观测变量\(yi\)遵循GPD分布，位置参数\(\mu\)固定，尺度参数\(\sigmai\)依协变量\(\mathbf{x}i\)以对数线性函数形式建模，即

\[
\log(\sigmai) = \mathbf{x}_i^\top \boldsymbol{\beta}
\]

形状参数\(\xi\)在所有样本中视为一致。推导了该模型的概率密度函数、尾部生存函数、条件期望和方差的表达式，强调模型能够刻画基于协变量变化的尾部分布特征。解释了极端负收益大于5%条件概率对于风险管理的重要意义。说明最大似然估计（MLE）在\(\xi<1\)时存在，以保证数学上的健全性。

引入四种贝叶斯先验：

• 截断Cauchy先验（\(\xi\)形状参数位于\(-\infty,1\)之间，上截断1保证条件期望存在）

- 回归系数\(\beta\)的Cauchy先验（重尾分布，弱信息先验，允许较大效应）

• Lasso先验（拉普拉斯分布，稀疏性促进，适用于变量筛选）

- Ridge先验（正态分布，连续收缩，适合所有变量均贡献微弱情形）

• Zellner的g先验（贝叶斯经典线性回归先验，基于设计矩阵结构，高效计算，适合模型比较）

作者阐述了MAP估计的优势——速度快、稳定，可作为全贝叶斯推断（MCMC采样）的精简初步筛选和模型探索工具，兼顾因先验带来的正则化效果，适合大数据或高维变量情况[page::2,3,4,5,6].

4. 频率学属性模拟研究

通过模拟数据对上述四种先验下的GPD回归模型进行性能对比，生成100个包含100个样本的数据集，含5个自变量。评估指标包含测试集预测RMSE，系数\(\beta\)和形状参数\(\xi\)估计误差RMSE，模型复杂度指标（AIC、BIC）以及计算成本。

模拟结果总结在表1中：

| 指标 | Cauchy | Lasso | Ridge | g-prior |
|------------------|---------|---------|---------|---------|
| RMSE (y) | 11.36 | 10.37 | 10.65 | 10.43 |
| RMSE (β) | 0.10| 0.16 | 0.16 | 0.18 |
| RMSE (ξ) | 0.08| 0.08 | 0.09 | 0.11 |
| AIC | 162.67| 177.15 | 175.74 | 180.94 |
| BIC | 176.97| 191.44 | 190.03 | 195.24 |
| 计算时间（秒） | 0.00 | 0.60 | 0.53 | 8.45 |
| 时间（相对Cauchy）| 1.00 | 175.64 | 155.69 | 2476.86 |

• 虽然RMSE(y)指标上Lasso和g-prior稍好些，但Cauchy先验在系数和形状估计准确度及信息准则（AIC、BIC）方面表现最突出，且计算效率最高。

- g-prior计算开销甚大，显著高于其他先验。

• Lasso倾向于产生过度稀疏，可能导致性能下降。

模拟结果说明Cauchy着重保持参数估计稳定性和模型简约性，兼顾泛化能力[page::6]。

5. 印度市场崩盘实证研究

实证选取Nifty 50日收益率中跌幅低于-2%的样本，在此基础上以绝对值定义严重跌幅，约占全部数据4.6%，其中11.6%跌幅超过5%。模型协变量包括Nifty的经验波动率与Garman-Klass波动率，以及标普500和黄金的相应波动指标，均标准化处理。

数据随机拆分为80%训练集和20%测试集，使用RMSE评估预测精度，AIC和BIC评估拟合优度。

表2模型评估结果：

| 先验模型 | RMSE | AIC | BIC |
|---------------|--------|----------|----------|
| Cauchy | 1.58| 298.06| 322.20|
| Lasso | 1.80 | 311.57 | 335.71 |
| Ridge | 1.73 | 302.07 | 326.20 |
| Zellner's g-prior | 1.94 | 308.12 | 332.25 |

• Cauchy先验模型在精度和信息准则指标中均为最优。

- Lasso模型表现较差，怀疑系过度收缩导致低估部分相关性。

利用Cauchy模型计算极端损失的条件期望和超额概率，发现波动率升高时，预期损失从2.4上升到7以上，极端亏损的概率从5%升至65%以上，呈现非线性关系。

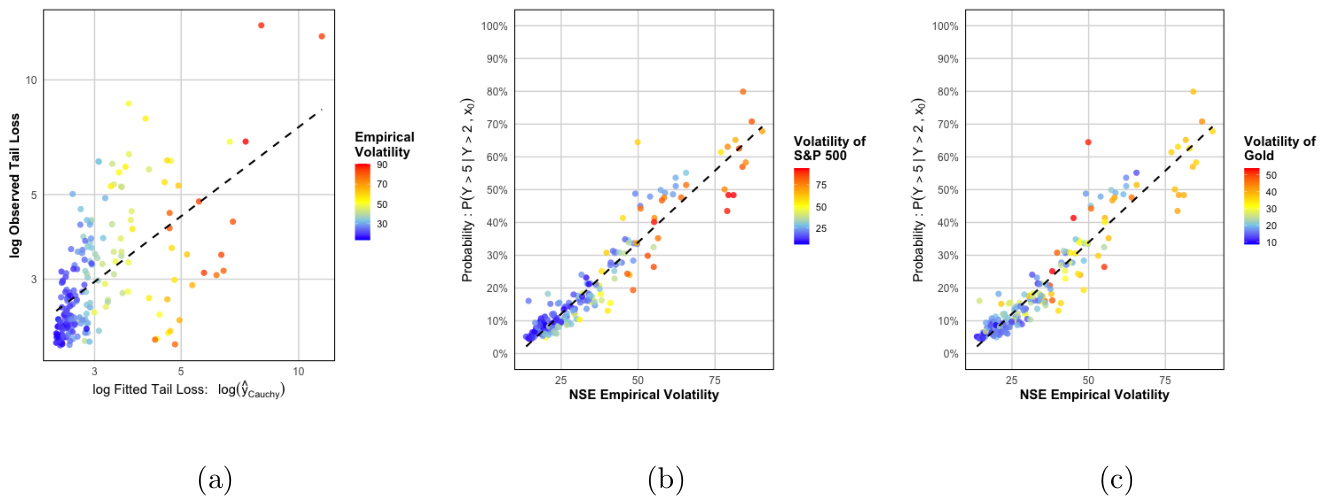
图3说明（含三幅子图）：

• (a) 测试集的对数观测值与拟合值散点图，颜色映射Nifty经验波动率，显示波动率越高，实际损失越大。

- (b) 和 (c) 分别展示了Nifty经验波动率与条件超额概率的关系，点色表示标普500和黄金波动率，点色梯度表现国际市场的溢出效应和避险特征。

• 这些图形直观展现了本模型能将本土和国际风险因子整合进尾部风险评估，为风险管理提供了可解释且动态的量化工具。

综合来看，实证结果支持了模型对印度股市巨额下跌风险的有效预测与解释能力，且强调全球因素不可忽视[page::7,8]。

6. 结论

• 本文创新性地将贝叶斯GPD回归模型应用于印度股市极端风险建模，将尺度参数作为市场波动性等协变量的对数线性函数，形状参数全局一致保证参数稳定。

- 通过模拟对比不同正则先验，验证了Cauchy先验在平衡预测精度与模型复杂度上的优势，并在实证中得到验证。

• 发现国内与全球波动率均对尾部风险显著影响，尤其是标普500表现为全球股市风险溢出，黄金体现避险需求，强调跨市场信息融入尾部风险分析的重要性。

- 模型能够反映非线性和交互效应，预测极端崩盘概率在高波动时超过60%。

• 研究方法和模型适合系统风险监控、压力测试和尾部风险管理，未来建议探索动态时间序列扩展、引入宏观经济因子、以及分层贝叶斯框架以模型形状参数的时间变动或潜在冲击。

整体结论认为贝叶斯GPR模型特别是配合重尾Cauchy先验构成有效优雅的尾部风险建模工具，适合新兴市场金融极端风险场景[page::8]。

图表深度解读

图1（第2页）

• 内容：Nifty 50的多维走势图：

- (a) 日收盘价走势，展示2007至2025年的长期上涨趋势及阶段性波动；
- (b) 日对数收益率及阈值(-2%蓝虚线，-5%红虚线)，表现出极端负收益集中出现的时间段如2008和2020年的剧烈跌落；
- (c) 基于EWMA计算的经验波动率时间序列，呈现多个波动峰值，贴合极端下跌时期；
- (d) Garman-Klass基于高低开收价的盘内波动率估计，波动强度波动更集中且峰值更高；
- (e) 经验波动率与Garman-Klass波动率散点图；
- (f) 同数据对数变换后散点图，相关系数约0.71，显示两种波动率估计方法相符且相互补充。

解读：图1系统呈现了Nifty 50市场价格与波动风险特征，统计指标与极端跌幅事件一致，且两种波动率度量在数值上高度相关，为后续模型协变量的合理选择提供数据支持。[page::2]

图2（第3页）

• 内容：三幅散点图展示Nifty 50极端负收益（大于2%和5%）与不同波动性指标的对应关系。

- (a) 自身经验波动率；
- (b) 标普500指数经验波动率；
- (c) 黄金经验波动率。

• 橘色虚线和红色虚线分别强调2%和5%阈值。

解读：

• 绝大多数极端亏损事件对应期波动率处于较高水平；

- 标普500波动率的影响尤为明显，显示全球市场波动具有溢出效应；

• 黄金波动率与极端亏损关联揭示避险需求增加。

这佐证了选择多市场波动率作为协变量的合理性及金融市场系统风险的全球关联特性[page::3]。

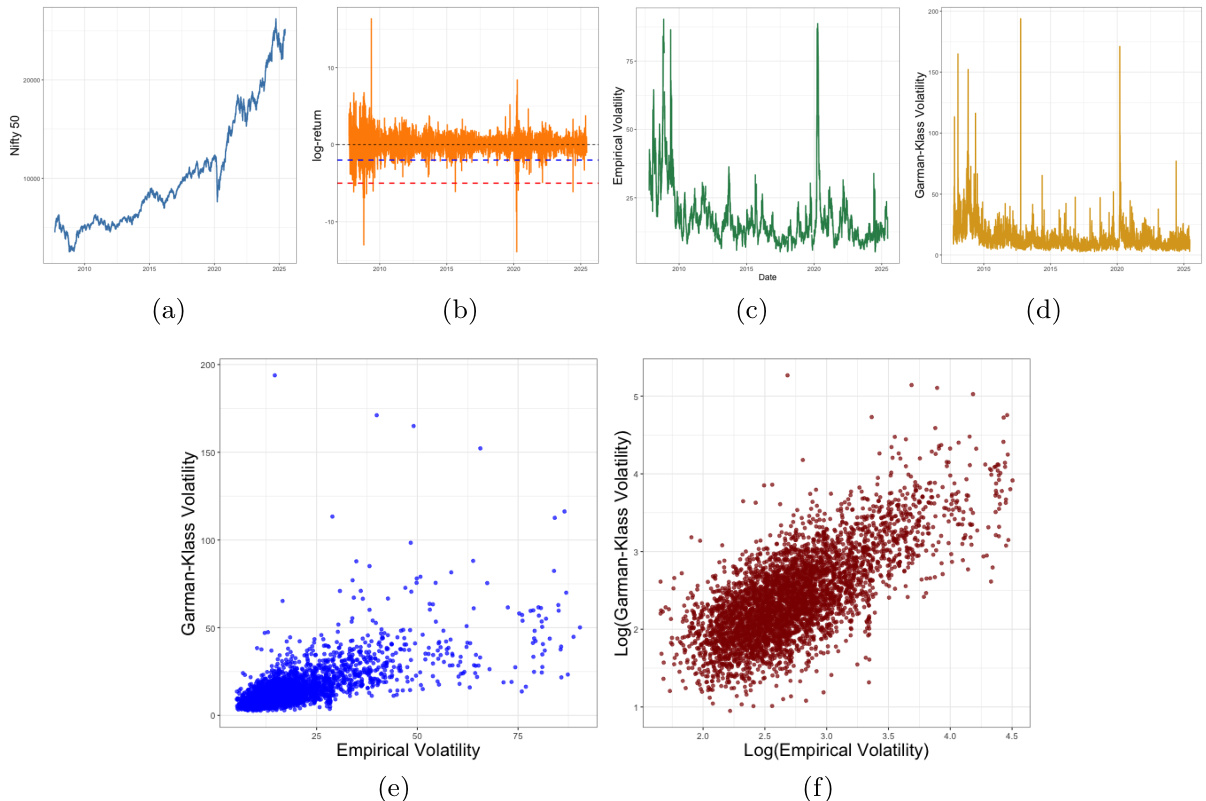
表1（第6页）

• 内容：模拟比较四种GPD回归模型先验下的表现，指标含预测RMSE、参数估计RMSE、AIC/BIC及运行时间。

解读：

• Cauchy先验在参数估计误差和信息准则均优于竞争者，含有更稳定的估计，且计算时间最短；

- 其他先验虽有时RMSE(y)较低，但参数RMSE及模型复杂度劣势明显；

• Webb-prior计算时间出乎意料地高，非适合大规模高频金融应用。

表格指示Cauchy先验适合动态风险评估及实时应用[page::6]。

图3（第8页）

• 内容：

- (a) 拟合与观测极端损失值的对数散点图，颜色映射Nifty经验波动率，呈现正相关趋势但尾部有较大分散；
- (b) 和 (c) 条件极端亏损概率与Nifty波动率关系，颜色反映标普500与黄金波动率，展示全球风险溢出和避险效应。

解读：

• 图(a)验证了GPD模型对极端亏损的拟合能力，体现波动率的风险放大效应；

- 图(b)(c)进一步揭示全球风险因子与本地极端风险的交互作用，强调包含全球波动指标提高预测能力。

这些图形直观表达了模型在复杂金融环境中对极端风险的描述能力与多变量联动特征[page::8]。

估值分析

本报告未涉及传统财务估值如市盈率或现金流贴现估值法，而是纯粹针对极端负收益的概率统计建模和预测，利用贝叶斯极值理论进行风险量化评估，因此不包含估值段落。

风险因素评估

虽然报告主要关注极端风险预测，但间接提及风险因素可总结为：

• 极端负收益的发生概率与市场波动率强相关，波动率急剧上升导致风险成倍增加。

- 市场间流动性冲击和波动率溢出效应，尤其国际股市（标普500）和避险资产（黄金）的波动率影响，加剧本地市场风险。

• 模型假设形状参数全局统一，可能忽略市场结构性突变或时变尾部行为，但模拟和实证验证限制了风险。

- 先验分布选择及参数估计稳定性对预测结果影响显著，显示模型设计需权衡复杂度和泛化能力。

• 计算开销差异大，尤其g-prior方案耗时巨大，实用性受限。

缓解策略体现在模型选择阶段采用重尾先验提高稳健性，并加入多市场波动指标加强预测质量[page::0,4,6,7,8]。

批判性视角与细微差别

• 报告对先验选择有明确偏好，尤推崇Cauchy先验，可能掩盖其他先验在特定情境的潜力和局限性。例如Lasso先验抑制部分变量的选择能力，虽有过度收缩，实则可能适用于噪声较多变量中筛选，未深入探讨其灵活应用。

- 形状参数假定为常数，有助解释性但忽略尾部厚度可能随市场环境变动，限制模型时间动态捕获能力。作者在结论中提及该方向为未来拓展，当前仍属限制。

• 模型只用波动率等几个市场指标做协变量，未整合宏观经济指标、政策变量或模型非线性扩展，加强模型预测解释的潜力仍存。

- 模拟数据基于理想多元正态协变量，现实数据协变量可能存在非正态性和异方差，模型在现实场景泛化风险未详述。

• 计算时间对比表现说明似乎Cauchy先验在优化时极高效，与传统理解中的重尾先验计算难度有所矛盾，可能跟具体实现和优化方法有关，值得进一步明确。

总体而言，报告清晰、严谨，但在一些假设与方法适用性边界及先验选择多样性探讨方面尚可深化[page::6,8]。

结论性综合

本报告通过构建并验证基于贝叶斯GPD回归框架的印度股市极端风险预测模型，成功将市场及国际波动指标引入极端尾部风险动态建模中。理论推导系统全面，涵盖参数己知与未知情况，详细说明概率分布及优良数学性质。模拟对比四种贝叶斯正则化先验，发现Cauchy先验在参数估计准确度、模型复杂度（AIC、BIC）和计算效率三个维度表现最优，能够有效避免过拟合与欠拟合的权衡难题。实证部分针对2007-2025年Nifty 50指数极端负收益数据，结合Nifty自身、标普500及黄金波动率，强化了模型的多市场动态响应能力，揭示全球溢出和避险驱动特点。

报告图形分析（图1、图2、图3）直观展现了数据特征及模型拟合性能，增进理解和沟通效果。具体分析指出在高波动时期，极端亏损概率及预期规模大幅上升，风险管理和策略制定必须关注波动率指标的动态变化。

综合来看，本研究在新兴市场尾部风险建模领域作出重要贡献，提供了一种既能保证模型可解释性又具备预测能力和计算效率的贝叶斯统计方法。未来工作如引入时变形状参数、宏观经济变量及层级模型，将进一步提升模型的现实适用性和政策指导价值。

---

以上是对报告的逐章剖析、图表解析、方法论细解及批判所作的全方位、深入且细致的分析，旨在为专业金融分析师、风险管理者和学术研究者提供全面的理解视角。[page::0–8]

报告