压缩性流体数值模型与实验数据对比验证 [page::0][page::1][page::2]

• 利用本土开发的hydRUB求解器，结合barotropic气穴模型，模拟超声波换能器两种实验装置。

- 模拟结果与水压计、影像法等实验测量数据在气泡体积、振荡频率与侵蚀区域分布上高度吻合。

• 采用统计学方法对固壁附近气穴塌陷事件进行归纳，量化流动侵蚀性。

不同网格分辨率对侵蚀概率影响及其表征 [page::1][page::2]

• 细、中、粗三种网格下侵蚀概率保持一致，说明模拟结果对网格敏感度较低。

- 侵蚀敏感区主要呈现环形分布，中间区域侵蚀概率较高，与实验表面损伤照片高度匹配。

• 侵蚀概率在较短的模拟时间窗口（约2ms）即可达到时间收敛。

超声波激励下气穴云的动态行为及压力波特性 [page::2]

• 模拟捕捉到随时间变化的气穴体积与压力波形，出现与实验中观测到的亚谐振荡频率（约5050Hz）一致的气泡振荡。

- 模拟压力峰值接近2-4巴的实验测量区间，气穴体积预测略低（约30%偏差），归因于实验测量方法假设。

负载集合与栅格依赖性分析 [page::3]

• 通过计算气穴塌陷事件的累积发生率与塌陷压力的关系，发现其呈指数衰减趋势。

- 对不同部位（换能器顶端与对样本）采用不同的标度指数κ（2/3与3/2）改善网格无关性，但不同区域的κ值不一，表明负载缩放规律存在空间差异。

• 模型可有效预测侵蚀敏感性，但需要进一步深入研究负载调节因子的准确性。

详细分析报告：《Numerical 3D flow simulation of attached cavitation structures at ultrasonic horn tips and statistical evaluation of flow aggressiveness via load collectives》

---

一、元数据与报告概览

• 报告标题： Numerical 3D flow simulation of attached cavitation structures at ultrasonic horn tips and statistical evaluation of flow aggressiveness via load collectives

- 作者与机构： S Mottyll & R Skoda，隶属于德国鲁尔大学（Ruhr-Universität Bochum）液压流体机械系

• 通信邮箱： stephan.mottyll@ruhr-uni-bochum.de

- 主题： 超声波喷嘴尖端附着气蚀结构的三维数值流动模拟，以及基于负载集合（load collectives）的流动侵蚀激烈度统计评估。

• 核心论点摘要： 本报告利用一种可压缩无粘流求解器结合拟压缩气蚀模型，针对两种不同的超声波喇叭检测装置开展三维气蚀流模拟，结果与水听器、水影像以及材料侵蚀测试数据对比，取得良好一致。通过对壁面邻近的单独气蚀塌陷事件的统计分析，提出负载集合表示流动的侵蚀激烈度，该集合呈指数衰减趋势，符合已知液压气蚀研究结果。该方法减小了网格依赖性，并针对瞬态壁面负载进行统计，成功预测气蚀敏感区域，实现了模型对材料侵蚀敏感度的有效验证。

- 研究目标： 验证自主开发的compressible CFD求解器hydRUB在“声学超气蚀”中的性能，及其侵蚀敏感区预测能力，同时创新性地将统计负载集合方法扩展应用于声学驱动气蚀情况。

• 重要贡献：

- 证实包含声学及液压特性的“声学超气蚀”可用compressible CFD方法准确模拟；
- 引入基于单事件塌陷负载的统计方法计算流动侵蚀激烈程度；
- 对气蚀敏感区域的统计分析与实验材料侵蚀结果高度吻合；
- 讨论并修正了数值网格依赖性问题。

---

二、章节深度解析

1. 引言

• 关键点总结：

- 超声波换能器尖端的气蚀现象为材料抗气蚀性研究的标准试验。
- 当喇叭尖端尺寸足够小且振幅高，超声激励频率下会形成大规模气蚀云，这些云体以自身的“亚谐波”频率（驱动频率的四分之一左右）振荡，称为“声学超气蚀”。
- 传统液压气蚀模型（基于Rayleigh方程的质量转移模型）因忽略了Rayleigh-Plesset方程的二阶导项限制，无法准确预测气蚀体积和亚谐波频率。
- Znidarcic等人发展了改进版的质量转移模型，对“声学超气蚀”的模拟准确。
- 本文作者采用另一种完全基于密度的可压缩CFD流动算法，能忠实捕捉与气蚀侵蚀直接相关的压缩波动力学。
- 同时，引入一种基于统计图式的瞬态壁面负载分析方法（此前已应用于液压气蚀的微通道和水翼件），对瞬态气蚀事件进行强度定量。

• 论证依据：

- 指出先前研究模型局限，提出采用compressible CFD的理由是捕捉可压缩波动，强化模拟真实性。
- 引用多篇国外标杆文献，确保理论和方法的学术连贯。

• 重要定义和技术术语：

- 声学超气蚀 (acoustic supercavitation)： 涉及气蚀云既有声学特性又兼具液压特性的复合气蚀形式。
- 负载集合（load collectives）： 单事件气蚀塌陷压力与累积事件频率的统计集合，表征流动侵蚀激烈程度。

2. 测试案例

• 关键点总结：

- 两个超声波喇叭试验装置，Case A与Case B，流动工况和几何尺寸均不同：
- Case A：喇叭尖端直径16mm，驱动频率19.82kHz，峰值振幅35.8μm，间距500μm，有对照样本。
- Case B：小直径3mm，驱动频率20kHz，峰值振幅164μm，参照Znidarcic 等实验。
- Case A为标准侵蚀测试，气蚀云填满空间，且振荡呈亚谐波周期，符合“声学超气蚀”特征。
- Case B扎根于高质量实验测量，包含高频水影像和水听器声学数据。

• 论证依据：

- Case A中侵蚀区域基于实验光学显微和共聚焦显微镜判断，并假设气蚀侵蚀高风险区对应气蚀体积和局部负载最大区。
- 对比过去数值研究，验证气蚀云行为模式。

3. 方法论与模型说明

• 3.1 数值及物理模型

- hydRUB：作者自主开发的三维密度基不可压缩流体力学求解器拓展为含低马赫数一致的Godunov格式处理可压缩无粘流体。
- 数值格式采用SMART和MINMOD重构技术，保证高精度流场变量解并减少数值震荡。
- 物理模型假定液体与气体（蒸汽）处于热力学平衡的均质混合物，忽略不可溶气体。
- 状态方程为“拟压缩”状态，等熵相变处理。

• 3.2 侵蚀分析流程

- 利用瞬态壁面压力与凝结速率结合构成复合侵蚀概率指标。
- 应用“Mihatsch等人提出的Collapse Detector”检测单独气蚀塌陷事件，提取塌陷压力强度。
- 应用基于球面波线性衰减的缩放定律，减少网格分辨率带来的负载与事件频率估计影响，缩放指数\(\kappa=2/3\)为参考值。

• 3.3 数值设定与验证

- 边界条件：滑移壁面，电脑网格跟随喇叭尖端运动。
- 自由液位采用对称边界和部分Dirichlet压力边界。
- 水温为室温。
- 流域网格采用双O型结构，对Case A实行网格敏感性研究，粗、中、精三种网格，单向尺寸均加密2倍，单个间隙单元数量依次从2.16万增加至138.2万。
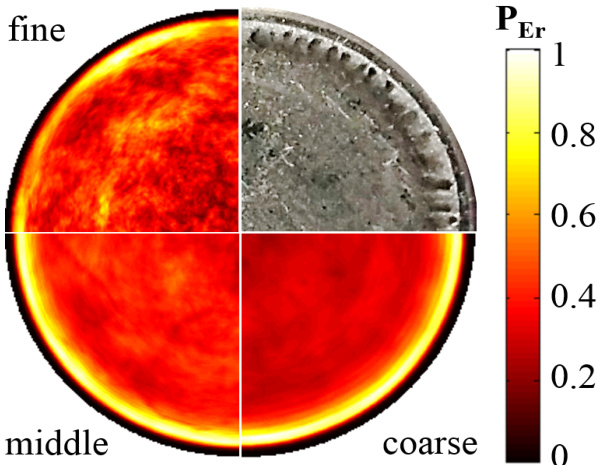
- 结果显示侵蚀概率在不同网格间一致：边缘区域概率最低，环带区域最高，中间区连续，且与材料表面侵蚀照片基本匹配（参见图1）。
- 气蚀云振荡特征及亚谐波周期均在各网格中再次验证。

---

三、图表深度解读

图1：网格数影响下的侵蚀概率与材料侵蚀照片对比

• 内容描述：

以热力图形式呈现不同网格细化程度（粗、中、精）计算的喇叭尖端侵蚀概率 \(P{Er}\) ，旁边配以实验侵蚀表面照片。能量条从0（黑色）到1（黄色）不等。

• 数据趋势与解读：

- 三种网格结果表现高度相似，均显示尖端边缘侵蚀概率最低，中间区域形成高概率的环形带。
- 实测侵蚀照片呈现明显的环状磨损区域，和模拟结果空间分布高度吻合，表明模拟方法对侵蚀位置预测准确。
- 这也表明网格加密对预测空间分布的影响有限，模型有较好数值稳定性和鲁棒性。

• 与文本联系：

文中说明，这种侵蚀概率分布支持该数值方法可靠捕获了物理过程，提示短时间模拟即可得出可靠的侵蚀统计数据。

---

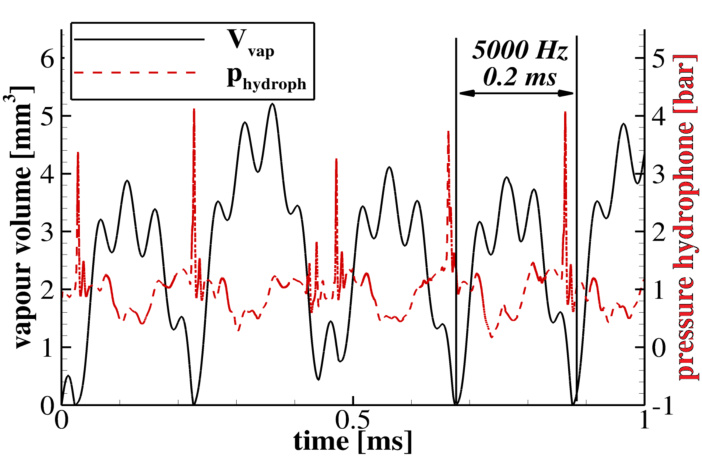
图2：案例B的模拟水听器压力与气蚀体积瞬态演化

• 内容描述：

时间区间内（1ms）气蚀蒸汽体积（\(V{vap}\)，立方毫米）和虚拟水听器压力（\(p_{hydroph}\)，巴）的瞬态曲线图。黑色实线为蒸汽量，红色虚线为压力。

• 数据趋势与解读：

- 点明气蚀体积最大约6.5 mm\(^3\)，压力峰值约4巴左右，最低时有蒸汽量归零节点。
- 同时，气蚀云振荡表现明显的亚谐波周期（约5000 Hz），反映与驱动频率20kHz相符的四分之一频率。
- 气蚀体积波动宽广，压力峰值尖锐且多次出现，反映出激烈的气蚀塌陷事件。

• 文本间隙补充：

- 数值模生成蒸汽量约为实验的70%（低估30%），可能为影像分析阈值处理及简化假设所致。
- 采用模拟的等值轮廓法更符合实验评估，更准确捕捉体积大小。

---

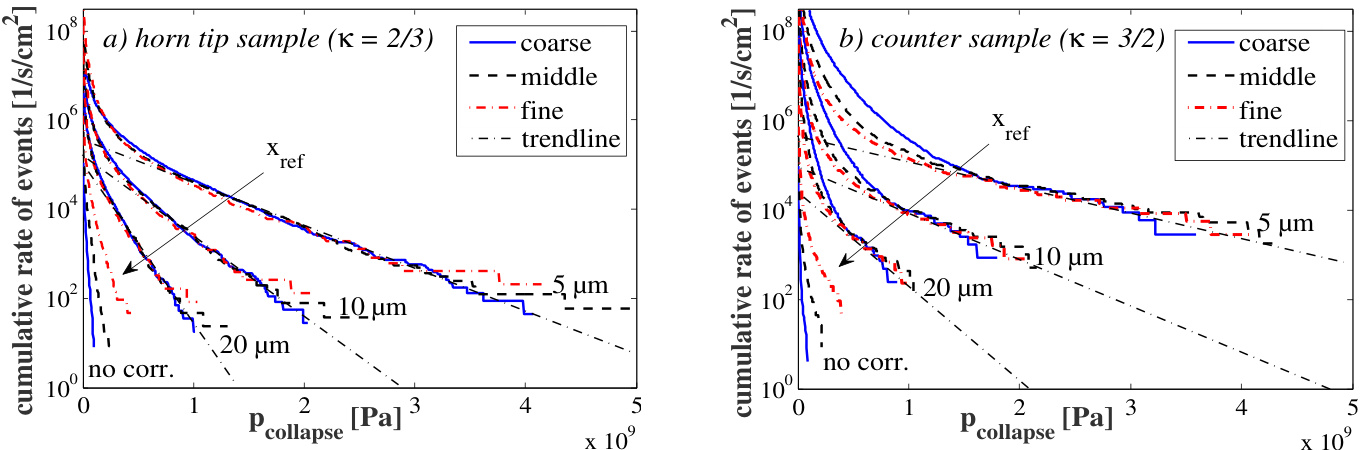
图3：负载集合曲线（堆积事件率 vs 气蚀塌陷压力）

• 内容描述：

- 左图为喇叭尖端100μm邻近壁面采样的负载集合图（以\(\kappa=2/3\)修正）；
- 右图为对应对照样本的负载集合图（以\(\kappa=3/2\)修正）。
- 颜色线条表示不同网格粗细，从粗网至细网逐级变化；包括未修正与修正后的数据及高压趋势线。横坐标为塌陷压力，纵坐标为累积事件率（log刻度）。

• 数据与趋势分析：

- 左图（喇叭尖端）经修正后不同网格负载集合曲线几乎重叠，显示网格修正方法有效消除了网格敏感性。
- 负载累积分布呈现指数衰减，表明高强度气蚀塌陷事件稀少但存在，符合液压气蚀经典统计规律。
- 右图（对照样本）则呈现较强的网格依赖性，低负载修正后仍差异较大，高负载模式需调整修正指数至3/2才有所缓解，但不同区域需不同\(\kappa\)，无法统一。
- 这种不统一带来无法同时比较二处负载的难题，且可能矛盾于实验界定的侵蚀热点。

• 与报告结论联结：

- 作者强调目前负载集合缩放指数并无统一值，且实例间存在差异，暗示后续需更深入研究与细化。
- 指出尽管统计方法强大，实际应用中需调整参数适应不同实验和流动结构特征。

---

四、估值分析（无）

本报告属于流体力学与气蚀数值模拟领域，无传统金融估值分析内容，故此部分不适用。

---

五、风险因素评估

• 风险识别：

- 数值模拟中网格依赖性是关键风险，尤其对对照样本区域负载统计和侵蚀预测影响较大。
- 采用的气蚀塌陷检测与负载集合缩放方法的参数\(\kappa\)不唯一，且表现出区域依赖性，影响结果可靠度。
- 蒸汽体积计算与实验相比存在偏差，可能因图像处理和模型简化产生误差。
- 壁面边界条件、流体假设（无不可溶气体）、温度恒定等限制了模型的适用范围和准确性。

• 缓解策略：

- 网格依赖问题通过系统网格加密和缩放比例调整进行缓解。
- 采集多网格数据并拟合趋势线，增强结果可用性。
- 对气蚀体积采用多种计算方法进行交叉验证。
- 持续开展对\(\kappa\)参数的深入研究以定位统一理论基础。

---

六、批判性视角与细微差别

• 潜在偏见与假设审视：

- 报告过分依赖了单一流动模型（无粘/可压缩/拟压缩模型），未充分讨论湍流模型选择对气蚀模拟的影响。
- 使用的假设如“不可溶气体被忽略”、均质混合物及等熵相变状态方程，均为理想化近似，可能限制复杂汽液两相流的真实表现。
- 对\(\kappa\)的选取依赖经验法则，缺少第一性原理解释，存在应用局限性。
- 蒸汽体积与实验有偏差，可能表明气蚀动力学中的局部瞬变过程尚未完全捕获。
- 网格敏感性虽在尖端区域得到良好解决，但对对照样本区域依旧依赖度高，影响对复杂形状与边界流动的泛化能力。

• 报告一致性：

- 在负载集合修正指数选择上，存在多个候选值且不同区域适用不同参数，体现了模型尚未完全成熟，报告对此持开放态度。
- 与实验对比中展示出对多数参数拟合较好，但对部分指标（如蒸汽量）未完全匹配，彰显数值与物理模型的精度边界。

---

七、结论性综合

本研究通过数值三维流动模拟结合统计分析方法，深入探索了超声波喇叭尖端典型“声学超气蚀”现象及其与材料侵蚀的关系。采用基于无粘可压缩流动的hydRUB求解器与气蚀塌陷检测装置有效再现了实验中观测到的气蚀云振荡、气蚀体积和压力脉动特征，特别是成功模拟了大规模附着气蚀结构的亚谐波频率振荡，证实了模型对声学与液压复合特性的捕捉能力。

统计负载集合方法拓宽了侵蚀激烈度定量手段，实现了对单个气蚀塌陷事件压力分布及其频率的概率统计，揭示出负载强度的指数衰减规律，符合已有液压气蚀的理论结果。吸收和改进网格依赖性修正方法后，本方法对侵蚀敏感区域的预测在定性和空间分布上均与实验侵蚀照片相符，展示强大预测潜力。

此外，报告指出负载集合缩放参数\(\kappa\)并非全局常数，不同区域表现差异，提示模拟复杂性与多样性并存，这也为后续研究留下了清晰的改进方向。

整体而言：

• 本文完整介绍了超声波引发气蚀的数值模拟与统计分析流程，验证并推广了侵蚀负载统计学方法。

- 模型与实验对比充分，方法可靠，能捕获关键物理现象。

• 细致的网格敏感性分析提升了数值结果的坚实性。

- 也诚实地承认了气蚀体积预测偏差、参数适用限制等存在问题。

这份报告对于数值模拟气蚀、超声波流体动力学及材料侵蚀机理研究领域具有较高的参考价值和理论启示意义。

---

参考文献

（报告全文中提供的15条相关领域参考文献支持理论背景与方法选择）

---

附图

1. 侵蚀概率网格敏感性图与材料侵蚀照片对比

1. 虚拟水听器压力与蒸汽体积瞬态演变（案例B）

1. 负载集合（累积事件率vs塌陷压力）示意图

---

【所有结论依据均来自原文各页内容，详见[page::0][page::1][page::2][page::3]】

报告