• 投资组合优化背景与风险测度选取 [page::0][page::1]：

- 现代投资组合理论依赖风险-收益权衡，Markowitz均值-方差模型假设正态分布，CVaR作为一致的风险测度更适合捕捉极端损失风险。
- 本工作采用CVaR（置信水平0.99）作为风险准则，结合时间序列模型与因子回归预测未来收益分布。

• 模型构建流程及因子选择 [page::4][page::5][page::6][page::7][page::8]：

- 先构建单资产ARMA-GARCH时间序列滤波器，提取标准化残差序列。
- 采用两类因子模型：稳健线性回归（RLR）和广义加性模型（GAM），将经济、技术及动量类20个因子作为解释变量回归残差。
- 因子覆盖范围包括Momentum（如RSI、价格动量）、Fundamental（如市盈率、市净率、EPS预测、ESG得分）、Technical（ATR、恐惧贪婪指数、赫斯特指数等）。
- 因子先归一化至[0,1]区间，GAM利用P样条捕捉非线性关系。

• 统计检验与因子显著性分析 [page::10][page::11][page::12]：

- GAM模型在拟合优度（调整后的$R^2$）、平均绝对误差（MAE）、BIC信息准则上均优于RLR。
- 对各因子显著性比率统计显示，GAM因子模型显著性更高，其中长周期RSI（30天）表现最佳。
- PCA分析显示GAM残差解释的非系统性方差更少，因子模型有效降低未解释风险。

• 投资组合样本外表现及风险调整收益对比 [page::13][page::14][page::15][page::16]：

- 三种模型：仅时间序列滤波器，无因子；加入RLR因子模型；加入GAM因子模型，均进行了基于不同风险容忍度参数（$\alpha$）的投资组合优化。
- GAM模型组合在总收益、年化收益及多种风险调整指标（信息比率、Sortino比率、Rachev比率、STAR比率和Gini比率）中整体领先。
- RLR模型虽能带来更高收益，但伴随极端风险与较大波动。
- 通过单独分组因子测试发现，综合使用所有三类因子（动量、基本面、技术指标）效果优于单独因子组。

• 策略适用范围与未来扩展方向 [page::16]：

- 研究在高效市场中取得积极效果，暗示该方法对低效市场亦有潜力提升。
- 未来可与其他机器学习模型如神经网络、支持向量机等比对，加纳更多因子以增强预测能力。

• 量化因子构建与策略总结 [page::4][page::5][page::6][page::7][page::8][page::13][page::14][page::15][page::16]：

- 因子模型基于ARMA-GARCH滤波后的标准化创新残差，回归解释变量为20个市场相关因子。
- RLR利用Huber与Tukey双权函数减弱异常值影响，GAM通过P样条建模非线性关系。
- 投资组合优化以均值-CVaR目标函数形式构建，包含无卖空限制和5%换手率约束。
- GAM因子模型提升模拟收益序列质量，进而改善均值-CVaR组合的样本外表现。

深度分析报告：《Enhancing CVaR Portfolio Optimisation Performance with GAM Factor Models》

---

1. 元数据与概览

报告标题：
Enhancing CVaR portfolio optimisation performance with GAM factor models

作者及机构：

• Davide Lauria，University of Calabria，Department of Economics, Statistics and Finance

- W. Brent Lindquist 和 Svetlozar T. Rachev，Texas Tech University，Department of Mathematics & Statistics

发布日期： 2024年1月2日

研究主题：
本文聚焦于金融资产组合优化，特别是基于条件风险价值（CVaR, Conditional Value-at-Risk）的投资组合优化方法，探讨将广义加性模型（GAM）应用于因子模型对提升CVaR投资组合性能的效果。

核心论点及目标：
作者提出一种离散时间的计量经济学模型，结合自回归滤波器和因子回归模型来预测股票收益，进而优化投资组合。研究同时对比稳健线性回归（RLR）和广义加性模型（GAM）两种因子模型在使用道琼斯工业平均指数（DJIA）和标准普尔500指数（S&P500）投资组合中的表现。核心发现显示，使用GAM估计因子模型能显著提升基于均值-CVaR目标的投资组合的超出样本表现。[page::0,1,3,4]

---

2. 逐节深度解读

2.1 引言与风险度量基础 (第0-1页)

引言回顾现代投资组合理论发展，强调投资组合优化是基于未来金融收益的随机过程进行的优化决策问题。传统的Markowitz均值-方差模型假定资产收益服从高斯分布，求解起来较为简单。为克服高斯分布假设的局限，文中引用了条件风险价值（CVaR）作为风险度量指标的优越性，特别强调了CVaR的“相干性”性质使其更具理论和实务应用价值。CVaR在实际中相较于均值-方差模型表现出更好的风险调整收益效率。[page::0,1]

2.2 投资模型理论框架与因子模型发展 (第1-2页)

作者论述了传统投资组合模型在实际运用时的若干瓶颈，如波动聚集、不对称厚尾分布以及交易成本和做空限制的影响。此外，提出采用基于经济金融解释变量（因子）提高对资产收益率的解释和预测能力，从而提升投资组合优化质量。文中回顾了经典的多因子模型历史，例如Rosenberg因子模型、CAPM与APT理论、Fama-French模型及其后续扩展。技术指标和动量策略的结合及其在收益预测上的潜力也被提及，指出技术分析虽受学术界质疑，但部分指标统计显著且结合机器学习方法表现优异。[page::1,2]

2.3 本文模型设计和方法流程 (第3-6页)

• 模型构造： 本文模型首先对每个资产收益率序列构建ARMA-GARCH滤波器，得到标准化创新序列。

- 因子回归： 标准化创新序列作为因变量，通过功能性回归函数 \(g(\cdot)\) 对20个技术、动量及基本面因子进行回归。

• 模型估计： 接口函数 \(g(\cdot)\) 设定两种形式：一是稳健线性回归（RLR），旨在缓解异常值影响；二是广义加性模型（GAM），允许非线性平滑函数自动拟合因子与收益的关系，提高模型灵活性。

- 联合分布拟合与蒙特卡洛模拟： 估计后收集多资产回归残差，拟合多元正态逆高斯分布（NIG），利用此分布生成未来收益模拟样本，供CVaR投资组合优化使用。

• 投资组合优化： 基于蒙特卡洛模拟收益样本，采用Rockafellar和Uryasev的线性化CVaR最小化方程计算投资组合权重，控制非负且权重和为1，不允许做空，同时考虑交易成本和调仓限制。

这一方法流程兼顾了收益预测的时间序列特征、因子驱动异质性及非高斯分布影响。[page::3,4,5,6]

2.4 因子选取细节 (第7-9页)

因子共20个，分为三类：

• 动量类（Momentum）: 包括不同窗口期的相对强弱指数（RSI）、6个月相对价格动量指标。

- 基本面类（Fundamental）: 市盈率（P/E）、市净率（P/B）、市现率（P/C）、市销率（P/S）及其5年平均比率，EPS预测及ESG评分。

• 技术分析类（Technical）: 平均真实波幅（ATR）、恐惧与贪婪指数（Fear & Greed）、Hurst指数（长期依赖）、新闻情绪评分和成交量。

所有因子均规一化至[0,1]区间。文中指出，该因子组合虽然有限但具有信息丰富性，足以改进模型超样本表现。文中后续章节也会验证单独因子类与全部因子合用对投资业绩的影响。[page::7,8,9]

2.5 超出样本表现与实证分析 (第10-14页)

• 数据范围和回测设置：

- 时间：2016年5月至2022年4月
- 标的：29只DJIA成分股（剔除新成分股Dow）和S&P500的96只代表性股票（以市值聚类降维选择）
- 模型估计采用765天滚动窗口，10,000次收益模拟，考虑双基点交易成本和5%换手率上限，无做空。

• 回归模型拟合比较（图1、2页）：

- 统计指标（调整后\(R^2\)、MAE、BIC）显示GAM对标准化创新的解释优于RLR。
- 各20个因子对应系数显著比例更高，尤其是动量类指标RSI30显著性最强。

• 主成分分析（图3页）：

- GAM残差相比单纯ARMA-GARCH创新显示更少被PCA捕捉的剩余方差，表明GAM因子模型有效减少未解释风险。

• 投资组合表现（图4及附表）：

- 不考虑因子的模型表现最弱。
- RLR因子模型虽提升总回报，但伴随极端风险（最大回撤和CVaR）升高，波动性高。
- GAM因子模型实现更高收益且风险指标平稳优异。
- 单因素类（动量、基本面、技术）单独回归均低于全部因子综合回归，提示多因子融合必要性。
- S&P500子集的测试结果一致验证上述结论，且RLR表现更差，GAM保持优势。[page::10,11,12,13,14]

2.6 讨论与研究展望 (第15-16页)

作者总结，将时间序列滤波器和因子回归采用广义加性模型（GAM）结合，能明显优化CVaR投资组合的超样本风险调整表现。GAM相比传统稳健线性模型（RLR）表现更稳定，风险回报比更优。该方法具有推广潜力，未来研究方向包括：

• 将GAM与神经网络、支持向量机、广义线性模型等其他机器学习模型做比较。

- 引入更多类别的因子来捕捉更全面的市场信息。

强调本文的贡献不仅在于投资组合优化技术的提升，更是在于金融领域首次将GAM成功应用于因子回归模型。[page::15,16]

---

3. 图表深度解读

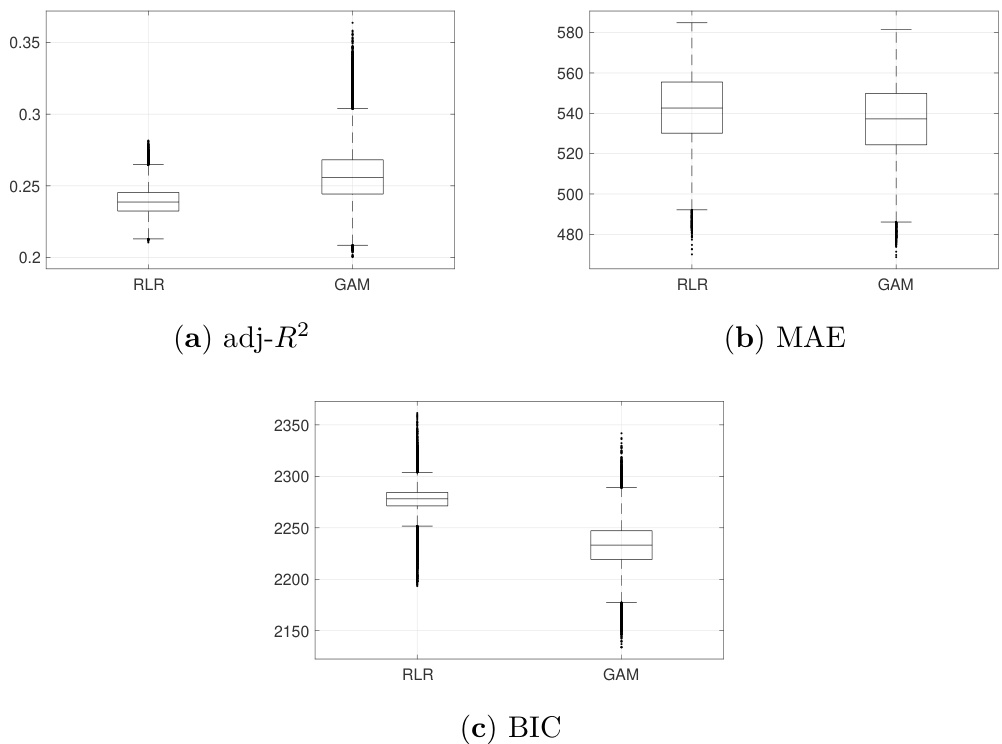
3.1 图1（第10页）

描述：
对29只DJIA股票日度因子回归的调整后\(R^2\)、平均绝对误差MAE和贝叶斯信息准则BIC三个统计指标的分布箱线图对比，展示RLR与GAM模型的表现。

解读与趋势：

• GAM的调整后\(R^2\)分布明显右移，表明模型解释力更强。

- GAM的MAE更低，拟合误差较小。

• BIC值，作为模型复杂度与拟合优度的综合指标，GAM更优。

综上显示，GAM因子模型在稳健性和解释力上均优于RLR。

联系文本：
支持作者关于GAM提升预测精度的论断，也是后续投资组合性能提升的基础。[page::10,12]



---

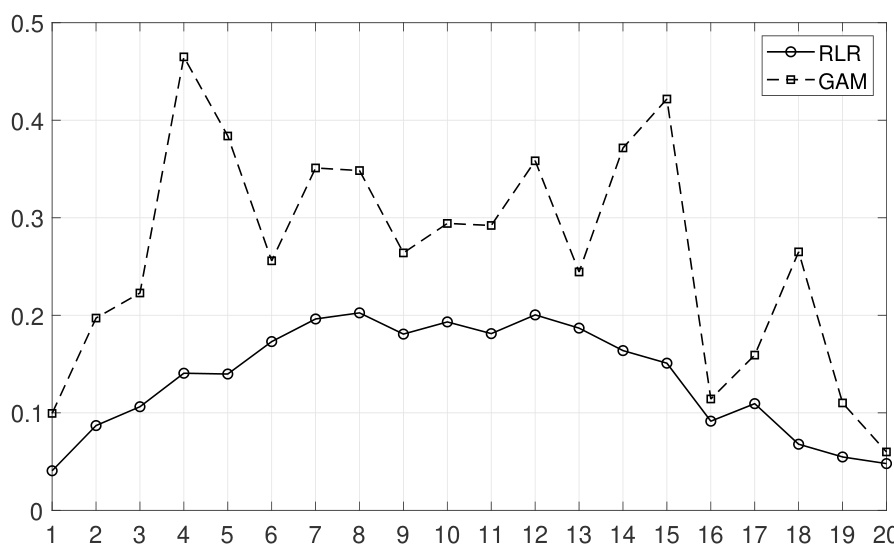
3.2 图2（第11页）

描述：
图示20个因子在所有资产及所有交易日回归中，达到显著性水平（p < 0.05）的比例。RLR用圆点线，GAM用方形虚线表示。

解读与趋势：

• 对所有因子，GAM显著回归的比例远超RLR。

- 动量因子RSI30天显著率最高，及时反映价格动量效应。

• 基本面因子整体也表现出较高显著率，显示传统财务指标信息强度。

- 技术指标的显著性相对较低。
这表明GAM能更好地把握变量与收益间的复杂非线性关系。

联系文本：
强化了作者关于GAM因子模型具备更强估计能力和解释力的结论，尤其对于动量因子的把握更准确。[page::11,12]



---

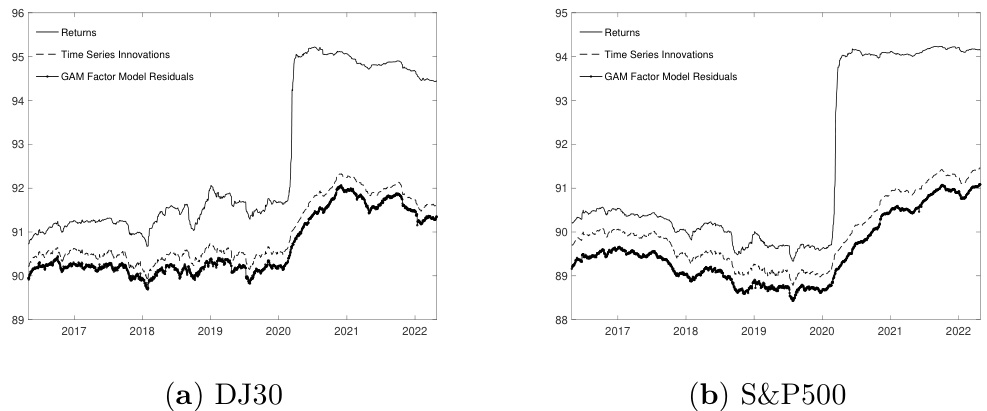
3.3 图3（第11页）

描述：
主要分解释方差占比随时间变动曲线，基于第一日三年滚动窗口内不同收益矩阵计算PCA得来。比较三个数据矩阵：原始简单收益（Returns）、ARMA-GARCH标准化创新（Time Series Innovations）、GAM残差（GAM Factor Model Residuals），对比两个市场（DJIA与S&P500）。

解读与趋势：

• 同样数量的主成分在模型残差中解释的方差降低，说明因子模型成功滤除系统性信息。

- GAM的残差解释方差最低，体现其更全面捕获了因子驱动影响，剩余波动较少。

• 该趋势在两个市场均成立，验证GAM模型泛化能力。

联系文本：
说明了GAM回归有效减少残余协方差矩阵中的结构信息，有助于投资组合风险更精确测度与管理。[page::11,12]



---

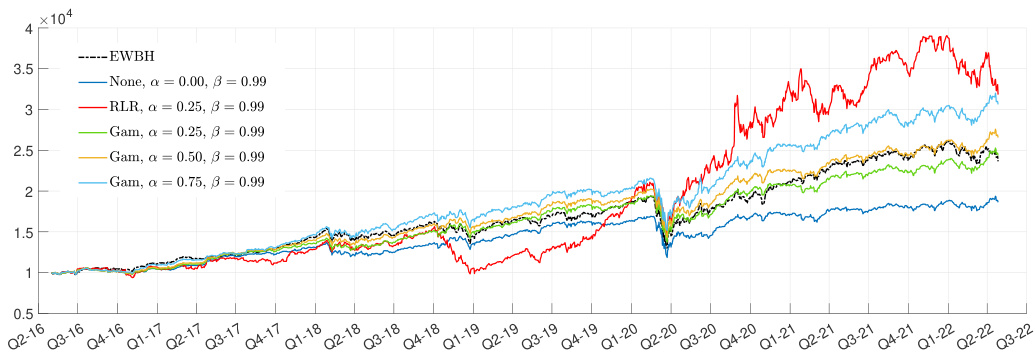
3.4 图4（第13页）

描述：
2016年5月至2022年4月，基于DJIA资产的超出样本投资组合价值演变曲线，对比无因子模型（None）、RLR因子模型、GAM因子模型及不动均等加权基准（EWBH）。

解读与趋势：

• 所有因子模型均优于无因子基线与EWBH。

- RLR因子模型初期表现落后且波动大，中后期回升迅猛但整体波动风险高。

• GAM因子模型则表现更加稳定，整体资产值增长更为平滑且最终价值最高。

- 提交不同风险偏好参数（α）时，GAM均表现一致优越。

联系文本：
该曲线直观体现了GAM因子模型不仅提供更好收益，还保持风险平衡，为实际投资提供强有力证据。[page::13,14]



---

4. 估值分析

本研究的估值并非传统意义上的公司估值，而是基于未来收益模拟的投资组合风险收益权衡。

• 采用的风险度量：条件风险价值（CVaR），参数显著性设置在99%。

- 投资组合优化目标：在均值（期望收益）与CVaR之间按风险偏好参数α加权，数学形式能够被线性规划方法高效求解。

• 驱动因素/假设：利用ARMA-GARCH捕获收益时间序列特性，通过因子模型捕获外生变量对性能的影响，再用多元NIG分布模拟资产相关性和尾部风险，生成场景供优化器使用。

- 因子模型增添的信息显著减少了残差中的系统性成分，提高了模拟精度，进而提升了投资组合配置质量。

---

5. 风险因素评估

报告中识别的主要风险因素包括：

• 模型假设风险：ARMA-GARCH及NIG分布假设可能无法完全拟合极端事件。

- 因子选择风险：有限20个因子可能未覆盖全部市场结构变化和潜在因子。

• 交易成本与限制风险：现实市场中，交易摩擦、调仓限制和做空禁令可能影响模型表现。

- 过拟合风险：尤其是GAM模型的平滑函数，如果平滑参数设定不当，可能在训练窗口表现优异但实际预测性能下降。
报告通过限制仓位、引入交易成本和设置调仓率上限，加以缓解部分风险，且超样本表现验证方法的稳健性。[page::5,10,13]

---

6. 批判性视角与细微差别

• 偏见及稳健性：

- 尽管GAM提供更优表现，但其灵活性也可能导致过拟合风险，尤其当因子信息变化或出现断层时，模型预测能力可能恶化。
- 因仅以两大成熟市场（DJIA、S&P500）为样本，结论可能不完全适用于效率更低或结构变化剧烈的市场。

• RLR模型表现波动过大，代表稳健线性回归未必能有效处理因子信息中复杂的非线性交互，值得进一步对比其他机器学习回归模型。

- 因子集限制： 排除宏观经济变量、某些流动性指标等，未来扩展因子范围可提升模型泛化能力。

• 报告结构层次清晰，但部分数学符号定义略显简略，可能增加初学者理解难度。

---

7. 结论性综合

本文系统地提出并实证验证了一种结合ARMA-GARCH滤波和因子回归的基于多元NIG分布模拟的CVaR优化投资组合方法。

• 相较于仅使用时间序列模型，加入因子模型显著改善了投资组合的超出样本表现，尤其是风险调整后收益能力。

- 在因子模型中，灵活捕获非线性效应的广义加性模型（GAM）较传统稳健线性回归（RLR）表现更优，具有更高的解释力和较低波动风险。

• 对动量、基本面和技术指标因子的综合使用优于单类别因子，展现了多元信息融合优势。

- PCA分析进一步证实GAM方法有效减少了收益创新中的结构性残差，提高了模型对资产相关性的解释能力。

• 投资组合表现定量指标（总回报、年化回报、最大回撤、CVaR、信息比率、Sortino比率等）均明显倾向于GAM方法。

- 本研究为传统投资组合优化提供了强有力的计量经济学方法论扩展，未来工作可探索更多机器学习模型和更广因子集合，期待将该思路推广到更加异质和效率较低的市场。

综上，作者明确推荐在CVaR投资组合构建过程中采用基于GAM的因子模型，以提升风险管理和收益表现，具有重要理论及实际应用价值。[page::0-16,20-25]

---

综述结束

本次分析详细拆解了论文的研究体系结构、方法论、数据处理和实证结果，特别强调了图表背后的数据故事和模型假设，并从风险和局限视角进行了客观评估。整体现代金融量化研究视角鲜明，对于金融工程、风险管理与资产配置研究者均具较高参考价值。

报告