克隆策略

Alpha系列——因子模型¶

不管是在现代的量化金融还是稍早的数量经济学领域，因子模型一直占据着核心地位。它不仅是对收益和风险的一个理想、简单的建模工具，还因为其有效性而备受理论界及工业界的青睐。在这篇教程中，我们将详细得阐述因子模型的理论基础和实践指南，并将结合金融市场的实际应用案例。

因子模型理论基础¶

基本符号和概念¶

\begin{align*} x_{i,t} &= \alpha_i + \beta_{1,i} f_{1,t} + \beta_{2,i} f_{2,t} + \cdots + \beta_{k,i} f_{k,t} + \epsilon_{i,t}\\ &= \alpha_i + \boldsymbol{\beta^{\prime}_i \cdot f_t} + \epsilon_{i,t} \end{align*}

其中：

$x_{i,t}$代表第i个资产在时间t的随机变量，如收益率
$\alpha_i$代表资产i的截距
$\boldsymbol{f_t}$表示共同因子，在不同的资产i之间保持常量
$\boldsymbol{\beta}$表示资产i的因子负荷，或者可以理解为因子$\boldsymbol{f_t}$的参数向量
$\epsilon_{i,t}$表示资产i的残差收益率，可以包含资产i的特异收益率

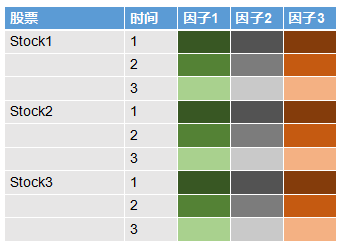
还记得在《Alpha系列——从MPT到APT》里，我们说到关于因子的概念么？大家可以从下面的图看到，左边的两列分别代表股票和时间，后三列代表的是三个不同的因子，图中因子下面的单元格的不同颜色代表不同值。不难发现，图中每个股票每个时间下面各个因子的颜色（值）是一样的，也就是说因子变量在不同股票间是共享的，每个股票的因子数据就是所有股票的共同因子数据，不过是在不同股票间重复而已。作为对比，我还列了一个一般意义上表示特征的表格，大家可以发现在特征表格中所有的值在一般意义上都是不同的。

上述因子模型的向量化版本为：

\begin{align*} \boldsymbol{x_t} = \boldsymbol{\alpha} + B \cdot \boldsymbol{f_t} + \boldsymbol{\epsilon_{t}} \end{align*}

其中B是因子负荷矩阵。

模型基本假设¶

模型假设1，$\boldsymbol{f_t}$是一个平稳过程：

\begin{align*} \mathbb{E}[\boldsymbol{f_t}] &= \boldsymbol{\mu_f}\\ Cov[\boldsymbol{f_t}] &= \mathbb{E}[(\boldsymbol{f_t - \mu_f})(\boldsymbol{f_t - \mu_f})^{\prime}] = \Omega_f \end{align*}

模型假设2，$\boldsymbol{\epsilon_t}$是一个白噪声过程：

\begin{align*} \mathbb{E}[\boldsymbol{\epsilon_t}] &= \boldsymbol{0_m}\\ Cov[\boldsymbol{\epsilon_t}] &= \mathbb{E}[\boldsymbol{\epsilon_t} \boldsymbol{\epsilon_t}^{\prime}] = \Psi\\ Cov[\boldsymbol{\epsilon_t},\boldsymbol{\epsilon_{t^{\prime}}}] &= \mathbb{E}[\boldsymbol{\epsilon_t} \boldsymbol{\epsilon_{t^{\prime}}}^{\prime}] = \boldsymbol{0} \quad \forall t \neq t^{\prime}\\ \end{align*}

其中，$\Psi$是一个(m x m)的对角矩阵，对角元素为$(\sigma_1^2, \sigma_2^2 \cdots \sigma_m^2)$。$\sigma_i^2$为第i个资产的残差风险（特异风险）方差。

模型假设3，$\boldsymbol{f}$与$\boldsymbol{\epsilon}$两两不相关:

\begin{align*} Cov[\boldsymbol{f_{i,t}},\boldsymbol{\epsilon_t}] &= \mathbb{E}[\boldsymbol{f_{i,t}} \boldsymbol{\epsilon_t^{\prime}}] = \boldsymbol{0}\\ \end{align*}

模型基本性质¶

条件矩：

\begin{align*} \mathbb{E}[\boldsymbol{x_t} | \boldsymbol{f_t}] &= \boldsymbol{\alpha} + B \cdot \boldsymbol{f_t}\\ Cov[\boldsymbol{x_t} | \boldsymbol{f_t}] &= \Psi \end{align*}

无条件矩：

\begin{align*} \mathbb{E}[\boldsymbol{x_t}] &= \boldsymbol{\alpha} + B \cdot \boldsymbol{\mu_t}\\ Cov[\boldsymbol{x_t}] &= B \Omega_f B^{\prime} + \Psi \end{align*}

值得注意的是，它们最大的差异在于方差部分，在因子是条件信息的情况下，不确定性仅由资产的特异风险构成；当因子信息不给定时，就有因子预测$\boldsymbol{\mu_f}$代替$\boldsymbol{f_t}$，从而引入了因子不确定性，所以资产收益的无条件方差等于因子不确定性加上资产的特异不确定性。

看过之前教程的读者可能会回忆起来，要估计$Cov[\boldsymbol{x_t}]$协方差矩阵，本身要估计$\frac{N(N-1)}{2}$个参数，而且参数估计误差使得协方差估计矩阵类似随机矩阵，只由少数特征值提供了大部分信息，这导致了实践应用的困难。而因子模型则拯救了我们，把估计整个协方差矩阵的任务分解成因子的协方差矩阵和资产的特异协方差矩阵。其中因子协方差矩阵的维度(K x K)要远远少于整个资产空间的维度(N x N)，而特异协方差矩阵是一个对角矩阵，所以说本质是一个N维向量，这使得协方差估计实践中变得可行。

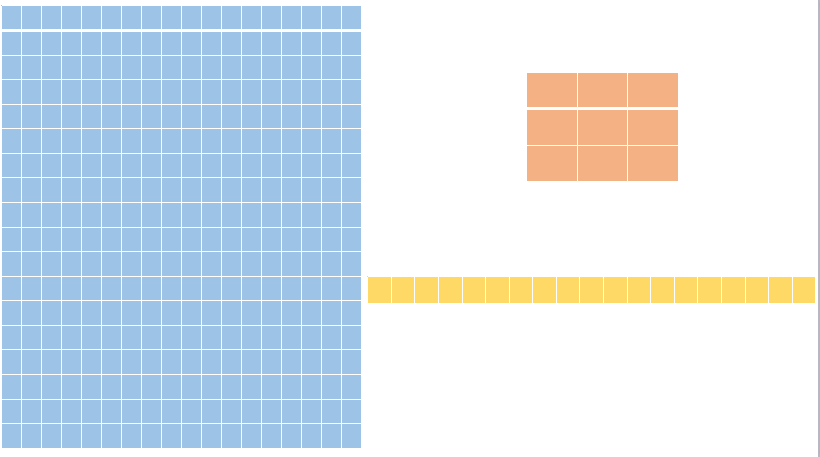
下面我画了一个示意图，蓝色的矩阵表示资产协方差矩阵，右边那个小矩阵代表因子协方差矩阵，绿色的则代表资产特异协方差矩阵的对角元素。可以看到，我们要估计的参数数量由原来的18x17/2变成了3x2/2加上18x1，一共是21个参数，减少到原来参数估计数量的14%左右。而在实际中资产数量要远远因子数量，假设由2000个资产数量，那么我们的参数估计比例将只有0.1%。

再论CAPM¶

CAPM把股票风险分解为系统风险和非系统风险：

\begin{align*} x_{i,t} = \alpha_i + \beta_i r_{m,t} + \epsilon_{i,t} \end{align*}

其中，$r_{m,t}$为市场在时间t的超额收益率，$x_{i,t}$为证券i在时间t的超额收益率，$\beta_i$是市场风险因子的暴露系数。

CAPM下的协方差矩阵¶

回顾我们之前的证明：

\begin{align*} \Sigma_x &= \boldsymbol{\beta \beta^T} \sigma_m^2 + diag(\sigma_1^2,\cdots ,\sigma_N^2)\\ &= \boldsymbol{\beta \beta^T} \sigma_m^2 + \Psi\\ &= \begin{pmatrix} \beta_1 \beta_1^T & \cdots & \beta_1 \beta_N^T \\ \vdots & \ddots & \vdots \\ \beta_N \beta_1^T & \cdots & \beta_N \beta_N^T \end{pmatrix} \sigma_m^2 + \begin{pmatrix} \sigma_1^2 & 0 & \boldsymbol{0} \\ 0 & \ddots & 0 \\ \boldsymbol{0} & 0 & \sigma_N^2 \end{pmatrix} \end{align*}

这里和我们上述的一般性因子模型的形式相同。

在下面的例子中，我随机选了5只股票，令中证800为市场指数，根据月收益率计算股票的月度beta系数。简单起见，假设无风险收益率为0。最后我们验证了直接计算X的协方差矩阵以及用因子模型来得到协方差矩阵，发现差异并不大。

In [100]:

start_date='2012-01-01'
end_date='2017-12-31'
instruments = ['601601.SHA', '600030.SHA', '601098.SHA', '600036.SHA', '000001.SZA']
index_col = '000906.SHA'
df = D.history_data(instruments+[index_col], start_date=start_date, end_date=end_date, fields=['close'])

# 重抽样还原至月度数据
resample_freq = 'M'
df_M = df.set_index('date')[['instrument','close']]\
                .groupby('instrument')\
                .apply(lambda df: df['close'].resample(resample_freq,how='last'))\
                .transpose()\
                .reset_index()\
                .set_index('date')

# 得到收益率数据
ret_M = df_M.pct_change().dropna()

In [112]:

from sklearn.linear_model import LinearRegression

X = ret_M[instruments]
r_m = ret_M[index_col]
reg = LinearRegression()
reg.fit(r_m.reshape(-1,1),X)
alpha = reg.intercept_
beta = reg.coef_
sigma2 = X.var()

In [115]:

import matplotlib.pyplot as plt

plt.plot(beta,alpha,'o')
plt.title('alpha vs beta')
plt.xlabel('beta')
plt.ylabel('alpha')
plt.show()

In [118]:

sigma2_m = r_m.var()
# 因子模型得到X协方差矩阵
Cov_X = np.outer(beta,beta)*sigma2_m + np.diag(sigma2)
Cov_X

Out[118]:

array([[ 0.01381715,  0.00839504,  0.00701413,  0.00416245,  0.00381665],
       [ 0.00839504,  0.04080852,  0.01255101,  0.00744824,  0.00682946],
       [ 0.00701413,  0.01255101,  0.03183812,  0.00622308,  0.00570608],
       [ 0.00416245,  0.00744824,  0.00622308,  0.01148666,  0.0033862 ],
       [ 0.00381665,  0.00682946,  0.00570608,  0.0033862 ,  0.01222547]], dtype=float32)

In [119]:

# 直接计算收益率协方差矩阵
X.cov()

Out[119]:

instrument	601601.SHA	600030.SHA	601668.SHA	600036.SHA	601098.SHA
instrument
601601.SHA	0.009126	0.011894	0.008541	0.006183	0.002736
600030.SHA	0.011894	0.025787	0.018179	0.010236	0.006174
601668.SHA	0.008541	0.018179	0.021352	0.008945	0.004770
600036.SHA	0.006183	0.010236	0.008945	0.007794	0.002372
601098.SHA	0.002736	0.006174	0.004770	0.002372	0.009121

Barra行业因子模型¶

模型形式¶

Barra行业因子模型可以由如下形式表达：

\begin{align*} x_{i,t} = \beta_{i,1} f_{1,t} + \beta_{i,2} f_{2,t} + \cdots + \beta_{i,K} f_{K,t} + \epsilon_{i,t} \end{align*}

向量化形式为：

\begin{align*} \boldsymbol{x_t} = B \cdot \boldsymbol{f_t} + \boldsymbol{\epsilon_t} \end{align*}

其中，

\begin{align*} \beta_{i,k} &= 1 \quad 表示股票i在行业k中\\ &= 0 \quad 其他情况 \end{align*}

$\beta_{i,k}$是事先知道的，$f_{k,t}$是不可观测的，是我们需要估计的参数，表示该行业因子在时间t的可实现收益率。另外x_{i,t}表示超额收益率，其他的模型假设和前面的因子模型相同。

模型参数估计¶

我们假设股票的行业是互斥的，即统一时间，一个股票只能属于一个行业，所以我们有：

\begin{align*} \boldsymbol{\beta_j^{\prime}} \boldsymbol{\beta_k} &= N_k \quad 如果 j=k\\ &= 0 \qquad 其他情况 \end{align*}

于是，我们可以得到行业实现收益率的OLS估计：

\begin{align*} \boldsymbol{\hat{f_t}} &= (B^{\prime}B)^{-1}B^{\prime} \boldsymbol{x_t}\\ &= \begin{pmatrix} \frac{1}{N_1} \sum_{i=1}^{N_1} x_{i,t} \mathbb{I}[\beta_{i,1}=1] \\ \vdots \\ \frac{1}{N_K} \sum_{i=1}^{N_K} x_{i,t} \mathbb{I}[\beta_{i,K}=K] \end{pmatrix} \end{align*}

相当于每个行业因子实现收益率等于该行业的平均超额收益率。

因子协方差矩阵：

\begin{align*} \hat{\Omega_f} &= \frac{1}{T-1} \sum_{t=1}^{T} (\boldsymbol{\hat{f_t} - \bar{f_t}})(\boldsymbol{\hat{f_t} - \bar{f_t}})^{\prime}\\ \boldsymbol{\bar{f_t}} &= \frac{1}{T} \sum_{t=1}^{T} \boldsymbol{\hat{f_t}} \end{align*}

收益率协方差矩阵：

\begin{align*} \hat{\Sigma_x} = B \hat{\Omega_f} B^{\prime} + \hat{\Psi} \end{align*}

实验探索¶

下面我们用python代码从0开始构建Barra行业因子模型，计算得到了行业因子收益率，并得到了股票收益率的协方差矩阵。在实验中，我们只包括了5个股票，在实践中，需要包含全行业的股票才能得到比较稳健的估计，在这个过程中需要处理股票行业迁移问题。另外，在实践中最好用迭代式回归得到近似解，我们实验中的解析解在实践中不太可行。

In [2]:

start_date='2012-01-01'
end_date='2018-12-31'
instruments = ['601601.SHA', '600030.SHA', '601098.SHA', '600036.SHA', '000001.SZA']
df = D.history_data(instruments, start_date=start_date, end_date=end_date, fields=['close','industry_sw_level1'])

# 重抽样还原至月度数据
resample_freq = 'M'
# 收益率矩阵
ret_M = df.set_index('date')[['instrument','close','industry_sw_level1']]\
                .groupby('instrument')\
                .apply(lambda df: df['close'].resample(resample_freq,how='last'))\
                .transpose()\
                .reset_index()\
                .set_index('date')\
                .pct_change()\
                .dropna()
# 得到行业矩阵
industry_code = df.set_index('date')[['instrument','close','industry_sw_level1']]\
                .groupby('instrument')\
                .apply(lambda df: df['industry_sw_level1'].resample(resample_freq,how='last'))\
                .transpose()\
                .reset_index()\
                .set_index('date')\
                .drop_duplicates()\
                .reset_index()\
                .drop('date',axis=1)\
                .stack()[0]

In [3]:

B = pd.get_dummies(industry_code,prefix='industry_').values
X = ret_M.values
F = np.linalg.inv(B.T.dot(B)).dot(B.T).dot(X.T)
Omega = np.cov(F,ddof=1)
errors = X-B.dot(F).T
Psi = errors.T.dot(errors)
Sigma = B.dot(Omega).dot(B.T) + Psi

统计因子模型¶

统计因子模型和经典因子模型最大的区别在于对因子的假设不同。在经典因子模型中，因子都是可观测变量，不管是CAPM/APT还是Barra模型；然而在统计因子模型中，因子是隐变量，隐变量是不可观测的。在统计学习或者机器学习的领域中，也被叫做隐变量模型。统计因子模型主要有两大类，分别是因子分析模型和主成分分析。

主成分分析¶

\begin{align*} \boldsymbol{x_t} &= \alpha + B \cdot \boldsymbol{f_t} + \boldsymbol{\epsilon_t}\\ &= \alpha + \Gamma_k \boldsymbol{p_k} + \Gamma_{-k} \boldsymbol{p_{-k}} \end{align*}

其中，$\Gamma_k$和$\Gamma_{-k}$分别代表前k个最大的特征向量和剩余的特征向量，同样地，$\boldsymbol{p_k}$和$\boldsymbol{p_{-k}}$分别代表前k个最大的主成分和剩余主成分。 $\Gamma_k \boldsymbol{p_k}$代表因子解释部分，$\Gamma_{-k} \boldsymbol{p_{-k}}$则表示残差部分。

对于$\Sigma_x$的特征分解：

\begin{align*} \Sigma_x &= P \Lambda P^{\prime}\\ PP^{\prime} &= \boldsymbol{I}\\ \Lambda &= diag(\lambda_1, \lambda_2, \cdots , \lambda_N) \quad \lambda_i从大到小排序 \end{align*}

P是我们的特征向量，$\Lambda$是我们的特征值。本质上PCA是一个降维技术，即从高维空间映射到它的子空间。如下图所示，我们可以通过子空间来最大限度得近似。

为了得到我们的特征向量和特征值，可以应用奇异值分解:

\begin{align*} X^* &= UDV^{\prime}, X^*表示中心化后的X\\ \hat{\Lambda} &= \frac{1}{T} D^2\\ \hat{\Gamma} &= U\\ P &= \hat{\Gamma}^{\prime} X^* = D V^{\prime} \end{align*}

下面的实验中我们利用前面的实验数据做了主成分分析，通过分析发现前三个主成分可以解释近80%左右的方差。同时，我们将主成分映射在2维的空间上，可以看到前两个特征向量的方向指向了X变动最大的方向。

In [50]:

X = ret_M.values.T
X_centered = X - X.mean(axis=1,keepdims=True)
T = X.shape[1]
U, d, VT = np.linalg.svd(X_centered,full_matrices=False)
V = VT.T
Lam = np.diag(d**2/T)
Gam = U
P = np.diag(d).dot(VT)
Sigma = Gam.dot(Lam).dot(Gam.T)

In [48]:

plt.bar(range(len(d)), np.cumsum(d)/d.sum())
plt.title("Explained variance of principal components",fontsize=20)
plt.ylabel("Explained variance",fontsize=20)
plt.xlabel("Principal Component",fontsize=20)
plt.xticks(range(len(d)), ['PC_' + str(i+1) for i in range(len(d))])

plt.show()

In [65]:

def biplot(X_centered,coeff,pcax,pcay,labels=None):
    pca1=pcax-1
    pca2=pcay-1
    xs = X_centered[pca1,:]
    ys = X_centered[pca2,:]
    m=X_centered.shape[0]
    scalex = 1.0/(xs.max()- xs.min())
    scaley = 1.0/(ys.max()- ys.min())
    plt.figure(figsize=(15,5))
    plt.scatter(xs*scalex,ys*scaley)
    for i in range(m):
        plt.arrow(0, 0, coeff[i,pca1], coeff[i,pca2],color='r',alpha=0.5) 
        if labels is None:
            plt.text(coeff[i,pca1]* 1.15, coeff[i,pca2] * 1.15, "Var"+str(i+1), color='g', ha='center', va='center')
        else:
            plt.text(coeff[i,pca1]* 1.15, coeff[i,pca2] * 1.15, labels[i], color='g', ha='center', va='center')
    plt.xlim(-1,1)
    plt.ylim(-1,1)
    plt.xlabel("PC{}".format(pcax))
    plt.ylabel("PC{}".format(pcay))
    plt.grid()

biplot(X_centered,U.T,1,2,labels=None)
plt.title('Principal Component in 2-D plot')
plt.show()

主成分分析总结：

主成分分析是一种降维方法，当股票数量很大时，通过主成分分析可以把股票收益率空间映射到一个子空间，这个子空间解释了股票收益率的大部分变异情况。主成分是对股票收益率的一种线性变换，变换过后的特征向量两两正交（不相关），并且特征向量按照特征值从大到下排列。我们需要确定选用多大的子空间纬度，即特征向量的数量来近似原始的收益率。还有一个特性就是通过降维，股票收益率的协方差复杂度也降低了，可以用K个特征向量来构造或者近似收益率协方差矩阵，而不需要估计完整的协方差矩阵。PCA是一种非监督学习算法，提供了另一种解释收益率的视角，然而在风险管理上，很难想象对特征向量进行风险中性化有什么实际意义。

因子分析模型(Factor Analysis Model)¶

传统因子分析有如下模型结构：

\begin{align*} \boldsymbol{x_t} &= \alpha + B \cdot \boldsymbol{f_t} + \boldsymbol{\epsilon_t}\\ Cov[\boldsymbol{\epsilon_t},\boldsymbol{\epsilon_{t^{\prime}}}] &= \boldsymbol{0} \quad \forall t \neq t^{\prime}\\ \mathbb{E}[\boldsymbol{f_t}] &= \mathbb{E}[\boldsymbol{\epsilon_t}] = \boldsymbol{0}\\ Var(\boldsymbol{f_t}) &= \boldsymbol{I}\\ Var(\boldsymbol{\epsilon_t}) &= \Psi \end{align*}

于是我们的收益率协方差矩阵为：

\begin{align*} \Sigma_x = B \cdot B^{\prime} + \Psi \end{align*}

因子分析模型比PCA要复杂一些，我们会另外专门写一篇ML系列的专题专门深入介绍因子分析模型，这里就大概说个总结。因子分析模型和PCA类似，它也是一种隐变量模型，实际上在ML的领域里，因子分析假设股票收益率X和隐变量$\boldsymbol{f_t}$都服从正太分布，然后B和$\Psi$通过EM得到近似解。

因子分析模型和PCA有很多相似之处，尤其是它们在模型架构上以及算法实现上。然而，它们也有本质的不同。PCA做的只是线性变换，换句话说，它只能捕捉线性特征，而不能捕捉到非线性特征。因子分析模型则不一样，它是基于隐变量的分布与观测分布的条件相关性，从某种角度可以理解为，它假设就是因为某些未知因素f而产生了结果x，但它们不必是线性的。所以因子分析的求解过程是基于EM算法，它是优化假设概率分布与实际分布的一种方法，从而能够捕捉到非线性效应。

总结¶

经典因子模型三大基本假设：
- $\boldsymbol{f_t}$是平稳过程
- $\boldsymbol{\epsilon_t}$是白噪声过程
- $\boldsymbol{f_t}$与$\boldsymbol{\epsilon_t}$两两不相关
共同因子在不同的股票间保持常数
收益率协方差矩阵可以分解为因子不确定性和残差不确定性，即$\Sigma_x = B \Omega_f B^{\prime}+\Psi$
CAPM是单因子模型，APT是多因子模型
Barra行业因子模型，是行业参数给定，行业因子收益率未知的因子模型
因子模型不仅是对收益率建模，也是对协方差的建模
统计因子模型是因子为隐变量的线性模型，一般分主成分分析和因子分析两类
主成分分析是非监督学习模型，也是一种降维方法，把收益率分解成正交特征向量，并按特征值从大到小排序
特征值解释了特征向量在股票收益率方差中的变异程度
因子分析是隐变量模型，它能捕捉隐变量和观测分布的非线性特征

Alpha系列回顾¶

参考文献¶

《OCW——Factor Modeling》
《Introduction to Machine Learning:Factor Analysis Models》
《Factor Models for Asset Returns》
《Machine learning A Probabilistic Perspective》
《The Fundamental Difference Between Principal Component Analysis and Factor Analysis》