前言¶
我曾与一个在印度连锁超市工作的运营经理聊天,讨论在节日前连锁超市应该准备的商品数量。对于他们而言,预测哪些商品会畅销,哪些商品会滞销非常重要。糟糕的决定会让客户回到竞争对手商店。面临挑战不止如此-需要估计的目标是不同品类商品的销售量,且商店处于不同位置,面临的客户拥有不同的消费手段。 当我的朋友描述这一挑战的时候,我内心作为数据科学家的一面开始微笑,因为我找到了下一篇文章的主题。在今天的文章中,我想介绍如何将回归模型应用到预测问题中,比如上文的这个问题。
一个让你大脑开始活跃的小训练¶
花一点时间列出可以想到的,一个商店的销售量需要依赖的因素。对于每个因素,提出一个假设:每个因子为什么以及怎样影响销售量。比如假设销售量依赖于商店位置,因为每个区域的居民有不同的生活方式。在Ahmedad的商店销售出去的面包量只会是Mumbai商店面包销售量的一个分数。
以同样的方式写下所有可能的因子:商店位置,商品供货,商店大小,产品价格,商品广告,商店布置,都可能是销售需要依赖的几个因素。
你能想到几个因子?对,不到15个,再想想!一个解决问题的数据科学家可能会想到上百个因子。
抱着这个念头,我想提供一个数据集——The Big Mart Sales。在数据集中,我们有多个连锁超市产品方面数据。
现在我们看一看数据集的快照:

在数据集中,我们可以看到产品特征(脂肪含量,可见性,类型,价格)和批发商店的特征(成立年份,大小,位置和类型)以及产品销售数量。我们看看是否能够使用这些特征预测销售量。
目录¶
简单预测模型
线性回归
最佳拟合直线
梯度下降
使用线性回归预测
评估模型$R^2$和校正$R^2$
使用所有特征预测
多项式回归
偏差和方差
正则化
岭回归
Lasso回归
弹性网络回归
正则化的不同方法
1. 简单预测模型¶
先从简单的方式开始。什么是预估销售量的最简单的方式?
模型1-平均销售量:¶
即使没有任何机器学习知识,如果你必须预测销售量,你也会提出这个方法-该销售量可能是过去几日/月/周的平均值。
这非常容易,但同样提出一个新的问题-这个模型有多好?
事实证明我们有很多方式可以评估模型,最常用方式是均方差。
预测误差¶
为了评估模型,先理解错误预测的影响:如果我们预测过高,商店会为了不必要的安排耗费很多钱,并导致多余的存货;如果预测过低,商店会失去销售机会。
最简单的评估误差的方式是评估预测值与实际值之间的差值。然而,如果我们简单将他们相加,可能会相互抵消,所以我们对他们求平方,然后相加。我们以数据点的数量相除来来计算平均误差,摆脱对数据点数量的依赖。
$$ \frac{e_1^2+e_2^2+……+e_n^2}{n}$$以上公式被称为均方差。
在这里,$e_1$,$e_2…$是实际值和预测值之差。
所以在第一个模型中,均方差是多少?对于预测所有数据点平均值的模型,均方差为2,911,799。误差很大,也许直接使用平均值预测的方式效果并不好。
是否能采取一些措施降低误差?
模型2-基于位置的平均销售量¶
位置对商品销售量影响至关重要。例如Delhi的汽车销售量一定比Vranasi的销售量高。因此使用“Outlet_Location_Type”(商店位置类型)这列数据进行分析。
基本方法为:计算每个位置类型的平均销售量进行预测。
该模型均方差为2,875,386,比之前的误差减少一些。通过使用一个特征“Location”(位置),误差降低。
如果有销售量相关的多个特征呢,如何通过这个信息来预测销售量?线性回归正好合适。
2. 线性回归¶
线性回归是用于预测建模中最简单和最广泛使用的统计工具。它基本遵循一个公式,将特征作为自变量,预测目标(销售量)作为因变量。
线性回归公式如下:
$$ Y = \theta_1x_1+ \theta_2x_2+…+ \theta_nx_n $$其中,$Y$为因变量(销售量),$x‘s$为自变量,所有的$\theta$为系数。系数是基于特征重要性,分配给不同特征的权重。例如,如果我们认为商品销售量相比较于商店大小更依赖于商店位置类型,这意味着一线城市的小店面会比三线城市的大店面销售量更高。因此,位置类型的系数 会比商店大小的系数更大。
因此,首先理解只有一个特征的线性回归,即只有一个因变量,公式为:
$$ Y = \theta_1x_1+ \theta_0 $$这是一个简单的线性回归公式,代表一条直线。$\theta_0$是截距,$\theta_1$的直线斜率。看一下销售量和MPR(最高零售价)的相关直线。

令人惊讶的是,我们看到商品的销售量与商品的价格呈正相关性。红点曲线代表回归曲线或者最佳拟合曲线,但是你如何发现这条曲线呢?
3.最佳拟合曲线¶
从下图可以看出,事实上存在很多曲线可用通过最大零售价来预测销售量。所以如何来决定最佳拟合曲线或者回归曲线?

最佳拟合曲线的主要目的是预测值与实际值或者观察值尽可能近,不应存在一个预测值与实际值相差甚远。换句话说,最小化预测值与实际值之差,即误差项。误差的图像特征如下。这些误差同样被称为残差。这些残差通过预测值与实际值之间垂直线表示。
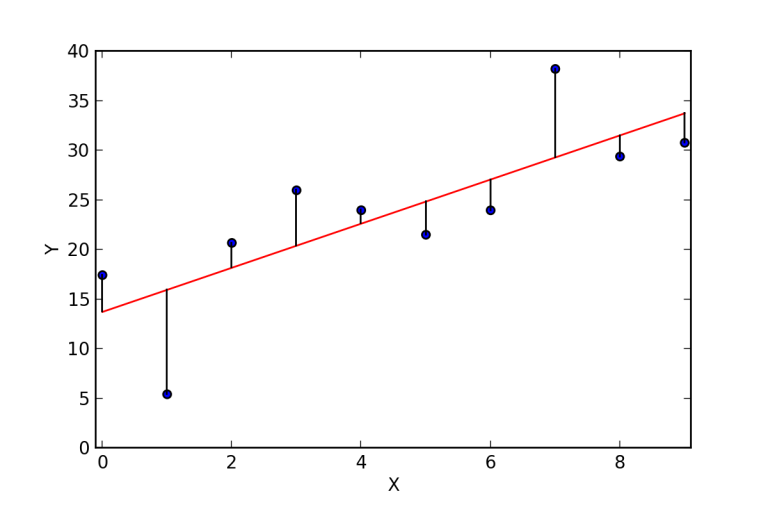
主要的目标是找到误差并使其最小化。在此之前,我们需要处理第一部分即计算误差。以下为计算误差的三种方式:
残差和$(\sum(Y-h(X)))$ 可能导致正负误差的相互抵消
残差绝对值和$(\sum|Y-h(X)|)$ 绝对值会防止误差的相互抵消
残差平方和$(\sum(Y-h(X))^2)$ 实际使用最多的方法,因为该方法惩罚大误差的力度大于惩罚小误差的力度,因此较大误差和较小误差对该公式值影响有很大的差别。同时该公式很好求微分,有利于选择最佳拟合直线。
因此残差平方和表示为:
$$ SS_{residuals} = \sum_{i = 1}^m(h(x)-y)^2 $$其中,$h(x)$是预测值,$h(x) = \theta_1x+\theta_0$,$y$是实际值,$m$是训练集中行数。
代价函数¶
举例说明:增大某个店铺的大小,预测销售量会增高。但即便增大了店铺大小,店铺销售量并未大幅度上升,所以用于扩大商店的代价得到负收益。
我们需要最小化这些代价,引入代价方程,用于定义和衡量模型的误差。
$$J(\theta_0,\theta_1) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2$$仔细看看这个方程,与残差平方和类似,只是多了乘以因子1/2m:为了降低数学上的处理难度。
为了改进预测,我们需要最小化代价方程。为了达到这个目的,需使用梯度下降算法。下面理解这是如何工作的。
4.梯度下降¶
考虑一个例子:找到下面方程的最小值。
$$ Y = 5x+4x^2 $$在数学中,求解关于x的方程导数,然后将其等于0,求得方程最小值的点位置。带入该值可以求得方程的最小值。
梯度下降也同样这样工作。它迭代更新$\theta$,找到代价方程最小值。如果希望深度学习梯度下降,推荐您阅读这篇文章。
5.使用线性回归预测¶
现在考虑使用线性回归来预测超市销售量。
模型3-编写线性回归¶
从之前的例子,我们知道使用正确的特征会提高模型准确度,所以现在使用两个特征:最大零售价格和商店建立年份来估计销售量。
Python语言建立一个线性回归模型,只考虑这两个特征。
# importing basic libraries
import numpy as np
import pandas as pd
from pandas import Series, DataFrame
from sklearn.model_selection import train_test_split
##import test and train file
train = pd.read_csv('Train.csv')
# importing linear regressionfrom sklearn
from sklearn.linear_model import LinearRegression
lreg = LinearRegression()
## splitting into training and cv for cross validation
X = train.loc[:,['Outlet_Establishment_Year','Item_MRP']]
x_train, x_cv, y_train, y_cv = train_test_split(X,train.Item_Outlet_Sales)
## training the model
lreg.fit(x_train,y_train)
## predicting on cv
pred = lreg.predict(x_cv)
## calculating mse
mse = np.mean((pred - y_cv)**2)
mse
该模型均方差为19,10,586.53,,比模型2更小。因此使用两个特征更加有效。
看看线性回归的系数。
# calculating coefficients
coeff = DataFrame(x_train.columns)
coeff['Coefficient Estimate'] = Series(lreg.coef_)
coeff
可以看到"最高零售价"有更高的系数,意味着价格越高,销量越好。
6. 评估模型$R^2$ 和 校正$ R^2$¶
模型有多精确,我们有评估因子来评估吗?实际上有一个定量方式,称为$R^2$。
$R^2$:决定$Y$(因变量)被$X$(自变量)解释的程度。数学上书写如下:
$$ R^2 = 1 - \frac{\sum(Y_{actual}-Y_{predicted})^2}{\sum(Y_{actual}-Y_{mean})^2} $$
$R^2$的值总是处于0到1之间,其中0意味着自变量并没有解释因变量$Y$,1意味着自变量能够完全解释因变量。
检查线性回归模型的$R^2$。
lreg.score(x_cv,y_cv)
$R^2$是32.8%,意味着销售量中的32%是由成立年份和最大零售价所影响的。换句话说如果知道成立的年份和最大零售价,就拥有32%的信息来准确地预测销售量。
现在想想,如果再引进一个特征,会发生什么,预测结果会更加精确吗,$R^2$值会增加吗?
考虑另一个例子:
模型4-使用更多变量的线性回归¶
我们已经了解使用两个特征会比使用一个特征得到销售量更精确的预测。
让我们引入特征“重量”(weight),用这三个特征建立回归模型。
X = train.loc[:,['Outlet_Establishment_Year','Item_MRP','Item_Weight']]
## splitting into training and cv for cross validation
x_train, x_cv, y_train, y_cv = train_test_split(X,train.Item_Outlet_Sales)
## training the model
lreg.fit(x_train,y_train)
运行结果报错,原因是“weight”(重量)这一列数据有一些缺失数据。让我们使用平均值来补充缺失数据:
train['Item_Weight'].fillna((train['Item_Weight'].mean()), inplace=True)
运行模型:
# importing basic libraries
import numpy as np
import pandas as pd
from pandas import Series, DataFrame
from sklearn.model_selection import train_test_split
##import test and train file
train = pd.read_csv('Train.csv')
## data preproccessing
train['Item_Weight'].fillna((train['Item_Weight'].mean()), inplace=True)
X = train.loc[:,['Outlet_Establishment_Year','Item_MRP','Item_Weight']]
## splitting into training and cv for cross validation
x_train, x_cv, y_train, y_cv = train_test_split(X,train.Item_Outlet_Sales)
## training the model
lreg.fit(x_train,y_train)
## predicting on cv
pred = lreg.predict(x_cv)
## calculating mse
mse = np.mean((pred - y_cv)**2)
mse
## calculating coefficients
coeff = DataFrame(x_train.columns)
coeff['Coefficient Estimate'] = Series(lreg.coef_)
coeff
lreg.score(x_cv,y_cv)
模型$R^2$为0.313。
校正$R^2$¶
$R^2$唯一的缺点是如果新的预测因子($X$)被添加到模型,$R^2$只会增加或者保持不变,但不会减少。我们不能对该变量进行判断:增加模型的复杂性后,模型更加精确吗?
这也是为什么使用“校正$R^2$”,校正“$R^2$”是$R^2$的改良,根据模型中预测因子的数量进行校正,考虑了模型的自由度。只有在预测因子改进模型精确度的时候,校正$R^2$才会增加。
$$R^2 adjusted = 1 - \frac{(1-R^2)(N-1)}{N-p-1}$$其中,$R^2$是R平方值,$p$是预测因子数量,$N$是所有样本数量。
7.使用所有的特征预测¶
现在我构造一个包含所有特征的模型。当构造回归模型的时候,需使用连续特征。将特征用于线性回归模型之前,分类变量需要被额外处理。这里有许多不同的方式处理,在这里,我使用一位有效编码。除此之外,将“商店大小”中的缺失值补充完整。
回归模型中数据预处理过程¶
# importing basic libraries
import numpy as np
import pandas as pd
from pandas import Series, DataFrame
import matplotlib.pyplot as plt
## import train data
train = pd.read_csv('Train.csv')
# imputing missing values
train['Item_Visibility'] = train['Item_Visibility'].replace(0,np.mean(train['Item_Visibility']))
train['Outlet_Establishment_Year'] = 2013 - train['Outlet_Establishment_Year']
train['Outlet_Size'].fillna('Small',inplace=True)
train['Item_Weight'].fillna((train['Item_Weight'].mean()), inplace=True)
# creating dummy variables to convert categorical into numeric values
mylist = list(train.select_dtypes(include=['object']).columns)
dummies = pd.get_dummies(train[mylist], prefix= mylist)
train.drop(mylist, axis=1, inplace = True)
X = pd.concat([train,dummies], axis =1 )
X = X.drop('Item_Outlet_Sales', axis=1)
构造模型¶
# importing linear regression
from sklearn.linear_model import LinearRegression
lreg = LinearRegression()
# for cross validation
from sklearn.model_selection import train_test_split
x_train, x_cv, y_train, y_cv = train_test_split(X,train.Item_Outlet_Sales, test_size =0.3)
# training a linear regression model on train
lreg.fit(x_train,y_train)
# predicting on cv
pred_cv = lreg.predict(x_cv)
# calculating mse
mse = np.mean((pred_cv - y_cv)**2)
mse
## calculating coefficients
coeff = DataFrame(x_train.columns)
coeff['Coefficient Estimate'] = Series(lreg.coef_)
coeff
# evaluation using r-square
lreg.score(x_cv,y_cv)
模型:均方差为:1,348,171.96,$R^2$为:0.548。
很明显,无论是均方误差还是$R^2$,都有很大的改进,意味模型能够得到更真实的预测值。
为模型挑选正确的特征¶
当我们拥有一个高维数据集,使用所有的特征会非常的低效,因为其中一些特征会引入冗余信息。我们需要挑选合适的特征集,构造精确的模型,有效地解释因变量。这里有几种方式去挑选特征集。首先,需要具备商业理解和专业知识。比如预测销售量时,我们知道市场推销 对销售量是个积极因素,也是模型中的重要特征。另外,自变量不应该相关。
相比较于手动挑选变量,我们可以通过前向或者后向选择来使过程自动化。前向选择从模型中影响最大的预测因子开始然后逐步添加变量。后向消除从模型中所有的预测因子开始,每步移除影响最小的变量。挑选原则可以被设置为任意统计方式比如$R^2$,$t-stat$等。
回归结果可视化详解¶
观察残差图像:
x_plot = plt.scatter(pred_cv, (pred_cv - y_cv), c='b')
plt.hlines(y=0, xmin= -1000, xmax=5000)
plt.title('Residual plot')

我们可以看到一个漏斗如图中形状所示。这个形状表明异方差性,误差项中的非常数方差导致异方差性。我们可以清晰地看到误差项(残差)的方差并不固定。一般来说,非常数方差主要来自于离群值或者极端杠杆值。这些数值拥有太多的权重,因此不成比例地影响模型性能。当这个现象发生 的时候,样本之外预测的置信区间会倾向于变得不切实际地宽或者窄。
我们可以简单地通过观察残差图像来检查这一点。如果异方差性存在,图像会呈现出一个漏斗形状,如上所示。这代表数据的非线性还未被模型捕捉到。我强烈推荐阅读这篇文章,对回归图像的假设和解释有详细的介绍。
为了获得非线性效果,我们有另一种回归类型比如多项式回归。现在开始学习吧。
8.多项式回归¶
多项式回归是另外一种形式的回归:自变量的最大影响超过1。在这种回归中,最佳拟合直线不是一条直线,而是一条曲线。
二次回归,或者二阶多项式回归,公式如下:
$$ Y = \theta_1+\theta_2x+\theta_3x^2$$看看下面的图:

显然二次回归公式相比于线性公式拟合得更好。在这个案例中,你认为二次回归的$R^2$的会比简单线性回归高么?答案显然是肯定的,虽然quadratic回归比线性回归能更好地拟合数据。当二次多项式和立方多项式普遍使用,但你同样可以添加更高次方的多项式。
下面这张图显示6次多项式形态。

所以你认为使用更高次方的多项式来拟合数据是更好的吗?不是,我们创建了一个可以拟合训练数据但是不能预测样本外数据的模型。因此,我们的数据在测试数据上表现很差。这个问题叫做“过拟合”,此时模型拥有高方差和低偏差。

同样地,另外一个问题叫做“欠拟合”,主要表现为模型无论在测试数据还是测试数据之外的新数据上都不能拟合良好。

当模型欠拟合的时候,模型具有高偏差和低方差。
9.回归模型中偏差和方差¶
偏差和方差是指什么?让我们通过一个射箭目标来理解这个问题。

我们有一个非常精确的模型,误差会非常小,意味着低偏差和低方差,如图1所示,所有的数据点都处于靶心中。同样地,如果方差增加,数据点的扩散也就增加,导致精确性变差。当偏差增加时,预测值和观察值之间的差值增加。
如何平衡偏差和方差以拥有一个完美的模型?看一看下图。

当我们添加越来越多的参数到模型中,模型复杂性提高,这会产生不断提高的方差和不断下降的偏差。即过拟合。所以我们需要找到模型的最优点,偏差的下降等于方差的提升。实际中,这里没有分析方法来找到这个点。所以,如何处理高方差或者高偏差?
为了克服欠拟合的问题,基本方法为:添加新的参数到模型上,模型复杂度下降,降低高偏差。
如何克服过拟合的问题?基本上有两种方式克服这个问题:
降低模型复杂度
正则化
在这里,我们详细讨论正则化,如何使用正则化将模型构造得更加通用。
10.正则化¶
我们已经完成了模型构造,预测,为什么还需要正则化?
假设你参加了一个比赛,在比赛中需要预测一个连续的参数。你使用线性回归然后得到预测结构。你现在在排行榜上。但是还有很多人在你之上。你做对所有事了吗?
我们希望能让方法变得简单,这也是我们为什么想要通过正则化优化我们代码的原因。
在正则化中,我们应该做得是保持同样数量的特征,但是减少系数j的量级,为什么降低系数能够有帮助呢?
让我们看看下面模型的系数。
predictors = x_train.columns
coef = Series(lreg.coef_,predictors).sort_values()
coef.plot(kind='bar', title='Modal Coefficients',)

我们可以看到Outlet_Identifier_OUT027 和 Outlet_Type_Supermarket_Type3的系数比其他系数更大,因此商品销售量更多由这两个参数决定。
如何降低模型中的系数量级?为了达到这个目的,我们有不同的回归方法,使用正则化来克服这个问题。
11.岭回归¶
首先检查一下上述问题,检查我们输出,无论它是否比我们线性回归模型表现更好。
from sklearn.linear_model import Ridge
## training the model
ridgeReg = Ridge(alpha=0.05, normalize=True)
ridgeReg.fit(x_train,y_train)
pred = ridgeReg.predict(x_cv)
## calculating mse
mse = np.mean((pred_cv - y_cv)**2)
## calculating score
ridgeReg.score(x_cv,y_cv)
模型均方差为1,348,171.96,$R^2$为0.5691。
我们的模型有一些改进,因为$R^2$增大了。注意alpha的值,这是岭回归的超参,该数值并不是自动从模型中学习得到而是手动设置。
考虑alpha的不同值,画出不同情况下的模型系数。




当我们提高alpha值,系数j的量级降低,甚至降低到零但不是绝对零值。
但如果计算不同alpha值情况下的$R^2$值,可以看到当alpha = 0.05时,$R^2$最大。因此我们需要通过在一系列数值范围之间重复这个过程来选择,然后找到误差最小的那个值。
所以你已经知道如何使用正则化补充,但看看数学方面如何处理。目前我们的想法还在最小化代价函数。
现在看看岭回归的代价函数:
$$ min(||Y-X(\theta)||_2^2+\lambda||\theta||_2^2) $$其中,我们添加了额外的项,被称为“惩罚项”。公式中的$\lambda$,实际上代表岭回归中的alpha值。通过修改alpha值,我们在控制惩罚项。alpha值越高,惩罚越强,因此系数量级降低。
重要知识点¶
岭回归收缩参数,因此主要用于防止多重共线性.
通过系数收缩降低模型复杂度
使用L2正则化方法
现在我们考虑另外一种使用正则化的回归方式。
12.Lasso回归¶
Lasso回归与岭回归十分相似,下面通过超市问题来理解两者的差异。
from sklearn.linear_model import Lasso
lassoReg = Lasso(alpha=0.3, normalize=True)
lassoReg.fit(x_train,y_train)
pred = lassoReg.predict(x_cv)
# calculating mse
mse = np.mean((pred_cv - y_cv)**2)
lassoReg.score(x_cv,y_cv)
结果为:均方差等于1,346,205.82,$R^2$等于0.5720
可以看到,均方差和$R^2$都增加。Lasso模型比线性和岭回归预测得更好。
另外,我们改变alpha值,看看它如何影响系数。


我们可以看到即使是一个很小的alpha值,系数量级降低很多。观察图像,你能够看出岭回归和Lasso回归的差异吗?
在岭回归中,当我们提高alpha的值,系数向零靠近。但在Lasso回归中,即使是更小的alpha,系数降至绝对零。因此,Lasso回归挑选一些特征当其设置为为零。这个性质被称作特征挑选,在岭回归中不存在。
Lasso回归背后的数学原理与岭回归很类似,差异仅仅是使用$\theta$的绝对值替代使用$||\theta||^2作为惩罚项。
$$ min(||Y-X\theta||_2^2+\lambda||\theta||_1) $$在这里,$\lambda$是超参,该参数相当于Lasso方程中的alpha。
重要知识点¶
使用L1正则化方式
当使用更多特征时,它能自动做特征挑选
当我们有一个大的数据集,比如我们现在有10,000个特征,一些特征是相关的。想一想,你会使用哪种回归,岭回归还是Lasso回归?
如果我们使用岭回归,它会保留所有的特征,系数会收缩。但问题是模型同样复杂,因为这里有10,000个特征,这会导致很差的模型性能。
代替岭回归,我们使用lasso回归。lasso回归的主要问题是当我们有相关联的变量,它会保留一个变量,将其他相关联的变量系数设置为0.这也许会导致一些信息的丢失,结果是模型精确度降低。
所以这个问题的解决方式是什么?实际上,我们有另外一种回归类型,叫做弹性网络回归,本质上是岭回归和Lasso回归组合,我们下面来学习一下吧。
13.弹性网络回归¶
在进入理论部分之前,让我们在超市销售问题中应用这一算法,它会比岭回归和Lasso回归性能更好么?让我们检查一下!
from sklearn.linear_model import ElasticNet
ENreg = ElasticNet(alpha=1, l1_ratio=0.5, normalize=False)
ENreg.fit(x_train,y_train)
pred_cv = ENreg.predict(x_cv)
#calculating mse
mse = np.mean((pred_cv - y_cv)**2)
ENreg.score(x_cv,y_cv)
模型均方差为1,773,750.73,$R^2$为0.4504
模型$R^2$值比岭回归和Lasso回归更小,你知道为什么吗?原因是我们没有大的特征集。弹性回归一般在有大数据集的时候工作得很好。
注意,我们有两个参数:alpha和l1_ratio。首先让我们讨论一下,在弹性网络中发生了什么,与岭回归和Lasso回归有什么不同。
弹性网络基本上是L1和L2正则化的组合。在弹性网络中,你可以通过调参来控制岭回归和lasso回归,公式如下:
$$ min(||Y-X\theta||_2^2+ \lambda_1||\theta||_1+\lambda_2||\theta||_2^2) $$如何调整$\lambda$以此控制L1和L2惩罚项?让我们通过一个例子来理解。你尝从一个池塘中抓到一条鱼,你只有一张网,然后你该做什么?你会随意投掷你的网吗?不会,你会等待直到你看到鱼在游动,然后你朝着那个方向投掷渔网,意图捕捉到整个鱼群。因此,即便数据 是相关的,你还是想要观察整个数据集。
弹性网络以同样的方式工作。数据集中有一大堆相关的自变量,然后弹性网络会简单形成包含相关变量的数据集。如果其中任何一个预测因子是一个很强的预测器(意味着与因变量有很强的关系),我们都会在构造模型时包含整个数据集,因为忽略其他的参数(比如在lasso回归中做的一样)或许会丢失一些具有解释能力的信息,导致一个很差的模型性能。
看看上面的代码,我们需要在定义模型的时候定义alpha和l1_ratio。alpha和L1_ratio可以分别帮助控制L1和L2惩罚项。实际上,关系如下:
$$ Alpha = a+b $$$$ l1\_ratio = \frac{a}{a+b}$$其中,$a$和$b$被分别分配给L1和L2项,所以当我们改变alpha和L1_ratio的值,$a$和$b$分别被设置,可以控制L1和L2之间的平衡:
$$a*(L_1 term)+b*(L_2 term)$$让alpha(或者$a+b$)$=1$,考虑一下例子:
如果l1_ratio=1,当且仅当$a=1$,$b=0$。因此,这是个lasso回归惩罚。
同样的,如果l1_ratio=0,暗示a=0。因此会是岭回归惩罚。
当l1_ratio等于0到1之间,惩罚为岭惩罚和lasso惩罚组合。
让我们调整alpha和l1_ratio,试着理解以下给定系数的图像:


现在,你对岭回归,Lasso回归和弹性回归有了一定的了解。但我们提到了L1和L2,这是两种类型的正则化。概括来说,lasso回归和岭回归分别是L1和L2正则化的直接应用。
想知道更多,请看下文。
14.正则化的不同方法¶
回想一下,在岭回归和lasso回归中增加惩罚项,但是惩罚项形式不一样。在岭回归中,我们使用$||\theta||^2$,在lasso回归中,我们是用$||\theta||$。所以为什么只能使用这两个呢?不能使用 其他的吗?
实际上,这里有其他正则化的可能选项,参数的阶数不同,表示为$\sum_i|\theta_i|^p$,称为$L_p$正则化。
现在以以2D形式对对正则化项画图。假设有两个参数,现在如果$p=1$,我们有$\sum_i|\theta_i|^p = |\theta_1|+|\theta_2|$。不同p值情况的画图如下:

在上图,轴坐标为$\theta_1$和$\theta_2$。让我们依次解释:
对于$p=0.5$,我们只能在一个参数极小时,得到另一个极大的参数取值。
对于$p=1$,我们得到绝对值和,其中一个参数$\theta$的增长会被另一个参数的下降抵消。
对于$p=2$,我们得到圆形。
对于更大的p值,我们得到圆方形。
我们使用的最普遍的正则化是$p=1$和$p=2$,被称为L1和L2正则化。
看一下下面的图画,蓝色为正则项,其他形状代表最小平方差或者数据项。

图1代表L1正则化,图2代表L2正则化。黑点表示最小平方差的点位置。我们可以看到它从该点移动,平方差呈二次方增长。正则化项在原点最小因为所有的参数为零。
现在的问题是哪个点导致我们的方程取值最小。答案是,如果他们呈二次方上升,两个项的和在它们第一次接触的时候最小化。
看一看L2正则化曲线,因为L2正则化的形状是一个圆,当我们远离他的时候,它呈二次方增加。L2最优点(基本就是接触点)停留在轴线上,只有当MSE最小值(均方差或者黑点)也取值在轴上。但对于L1正则化,L1最优点可以在轴上因为他的轮廓很峰利, 因此有很高的机会接触点降落在轴上。因此它有可能在轴线相交,即使最小MSE不在轴线上。如果相交点在轴上,被称作“稀疏的”.
因此,L1提供一定程度上的稀疏性,使我们的模型更加有效存储和计算,帮助检查特征重要性,因为不重要的特征系数会被设置为0.
结束语¶
我希望读者能够了解线性回归后的科学,补充并进一步优化。
“知识是宝藏,练习是找到宝藏的钥匙”
因此,开始做一些练习吧。你可以从超市销售量问题开始,通过一些特征工程的方法优化模型。
原文:《A comprehensive beginners guide for Linear, Ridge and Lasso Regression》