ML系列——PCA特征组合¶

PCA方法简介¶

这个方法使用股票的历史量价数据，在N个股票的横截面上向前追溯M天。在原始的Avellaneda的论文中，他假设所有的横截面都是完全一致的，然而在实践中，这个假设是不靠谱的，比如沪深300的成分股会随着时间的变化而变化。

我们定义股票在任意给定的时间点上$t_0$，往前追溯M+1天的收益率矩阵：

$$R_{ik} = \frac{S_{i(t_0-(k-1)\Delta t)} - S_{i(t_0-k\Delta t)}}{S_{i(t_0-k\Delta t)}}, k=1,\cdots,M, i=1,\cdots,N$$

其中$S_{it}$代表股票i在时间t上的复权价格，$\Delta t = 1/252$。因为股票收益的波动性，我们还需要将其进行标准化。

$$Y_{ik} = \frac{R_{ik}-\bar{R_i}}{\bar{\sigma_i}}$$

其中：

$$\bar{R_i} = \frac{1}{M} \sum_{k=1}^{M}R_{ik}$$$$\bar{\sigma_i}^2 = \frac{1}{M-1} \sum_{k=1}^{M}(R_{ik}-\bar{R}_i)$$

我们的经验相关系数矩阵定义如下：

$$\rho_{ij} = \frac{1}{M} \frac{\sum_{k=1}^{M}(R_{ik}-\bar{R_i})^2}{\bar{\sigma_i}^2}, 其中\rho_{ii}=1$$

在选用沪深300股票池的情况下，$\boldsymbol{\rho}$的维度是300x300，往往我们有用的数据量要远远小于我们需要估计的参数，在我们沪深300的具体例子里，参数数量是45150。事实上，如果我们考虑用每日收益数据，非常长的数据长度在实际中不一定有意义，市场的波动、股票的相关系数都在变动，那么其中一个选择就是使用滑动数据窗口。

一般比较常用的方法是对相关矩阵进行建模，我们对后验相关矩阵进行SVD分解得到特征值和特征向量，并按照如下顺序排列：

$$N \ge \lambda_1 \ge \lambda_2 \ge \lambda_3 \ge \cdots \ge \lambda_N \ge 0$$

我们的特征向量也按照上述顺序排列：

$$\nu^{(j)} = (\nu_1^{(j)}, \cdots, \nu_N^{(j)}), j = 1,\cdots, N$$

我们来看下针对2017年沪深300的pca分解，来看下特征数量与方差解释程度的关系：

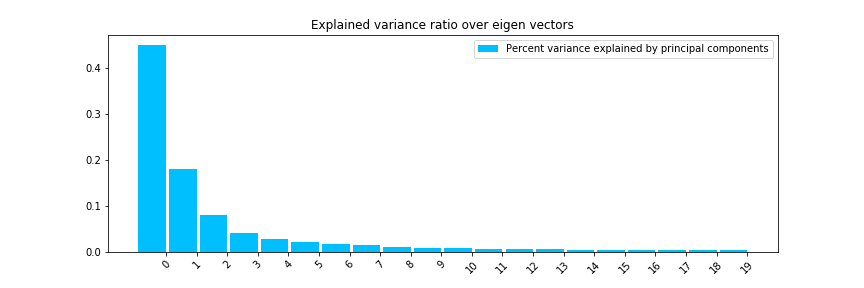
我们可以看到前三个特征向量解释了超过80%的变异方差。

我们称上述这些$\lambda_1,\cdots,\lambda_m,m < N$为显著的特征向量。每一个特征向量，我们都认为它是一个特征股票组合，在组合中每只股票的权重定义如下：

$$w_i^{(j)} = \frac{v_i^{(j)}}{\sum_{i=1}^N v_i^{(j)}}$$

于是，每一个特征组合的收益率为：

$$F_{jk} = \sum_{i=1}^N w_i^{(j)} R_{ik}, j=1,2,\cdots,m$$

我们来分别看下前两个特征向量的组合构成，首先是第一个特征组合：

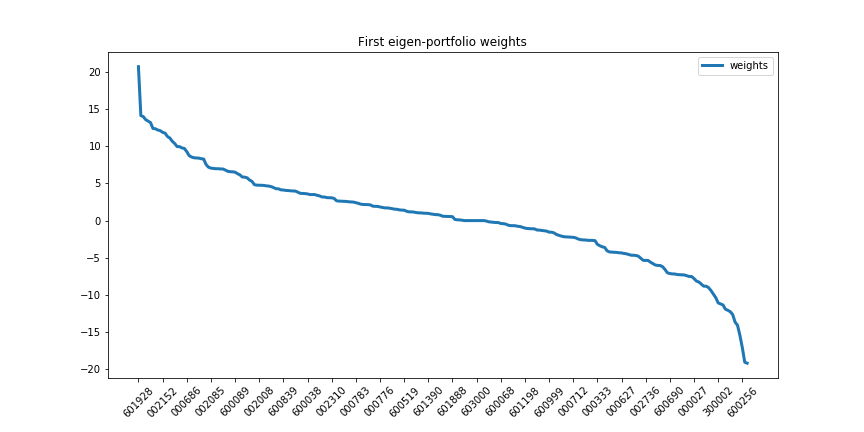
第二个特征组合：

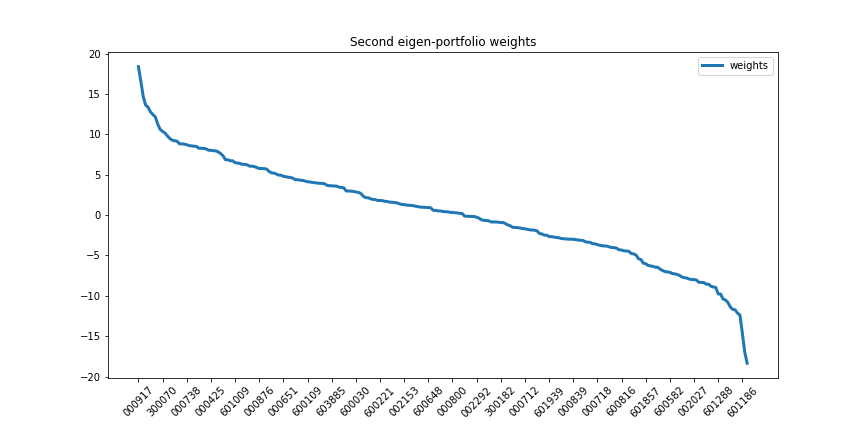
根据论文的解释，特征组合之间的收益是不相关。每一只股票收益都可以被分解并投射到m个特征因子和残差上，于是PCA提供了一种很自然的方式构建风险因子。很容易，我们可以证明相关举证可以分解为一个秩为m的矩阵以及一个满秩的对角矩阵：

$$\bar{\rho}_{ij} = \sum_{k=0}^{m} \lambda_k \nu_i^{(k)} \nu_j^{(k)} + \epsilon_{ii}^2 \delta_{ij}$$

其中$\delta_{ij}$是Kronecker delta,

$$\epsilon_{ii}^2 = 1 - \sum_{k=0}^{m} \lambda_k \nu_i^{(k)} \nu_j^{(k)}$$

这意味着我们只需要少量显著的特征向量再加上一个对角的“噪音”矩阵就可以解释市场的总体方差。

策略实现逻辑¶

现在来介绍下我们的PCA策略实现逻辑。

因为PCA是非监督学习，主要是做特征的“映射”，所以我们不需要太长的历史数据，我们选取2016年到2017年底共两年的沪深300股票前复权数据。同时我们采用滚动训练的方式去训练我们的PCA，每次选取6个月的训练数据来训练模型，然后应用在后六个月的测试数据上，大致思路如下图所示：

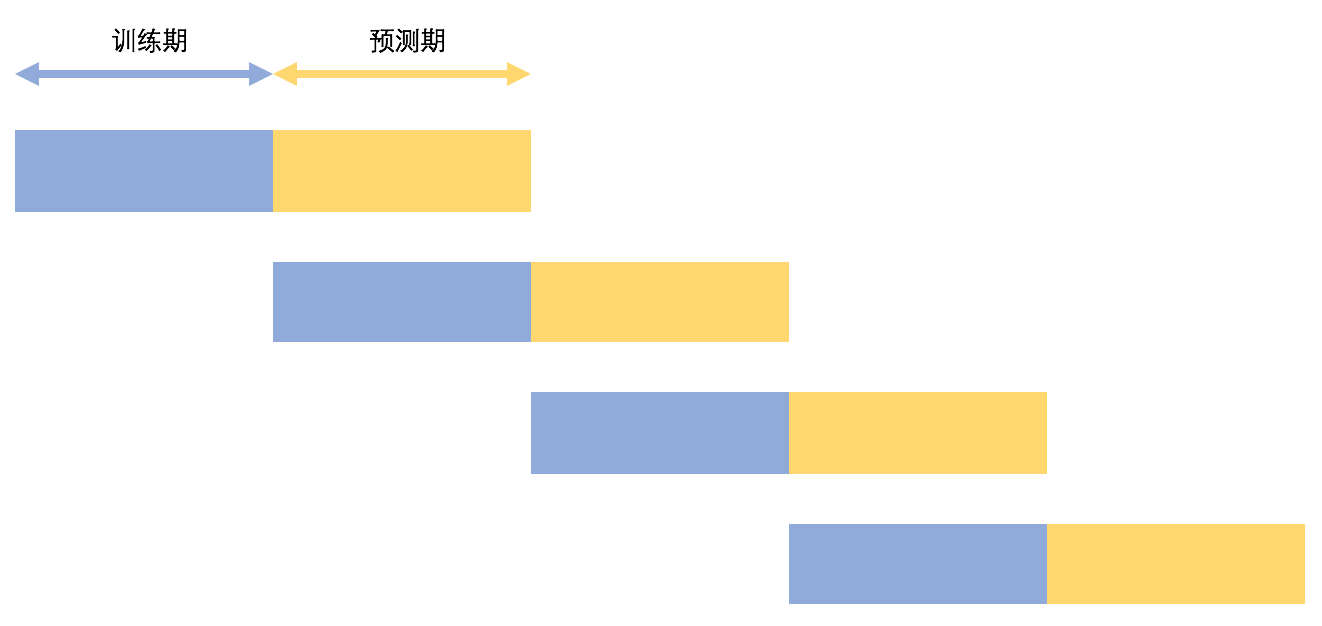
每个训练期，我们都会更新指数列表，因为数据成分可能在这个期间内发生变化。然后我们还注意到历史越长的数据实际上对未来的影响关系越来越弱，所以我们会对股票收益率进行指数加权，以突出最近的数据权重。

最后就是在每个训练周期内，如何去选取特征向量的数量了，因为我们观察到在不同时间周期内，主成分数量对解释变异程度存在比较大的差异。所以我们采取动态调整的方式，我们选取70%的方差变异解释率作为阈值，每次只选取刚好大于70%的特征向量的数量，这样也有助于防止对噪音的拟合。还有一个小细节的就是我们发现在某些情况下，特征向量的绝对值会非常大，这导致我们的特征组合拥有难以置信的组合杠杆，所以我们也对单只股票最大杠杆率做了最高3倍的限制，最终的组合权重是这些被选特征组合的加权，所以总杠杆不会这么高，但是注意，我们最终的特征组合仍然是一个多空组合。

下图是我们在训练期上的表现：

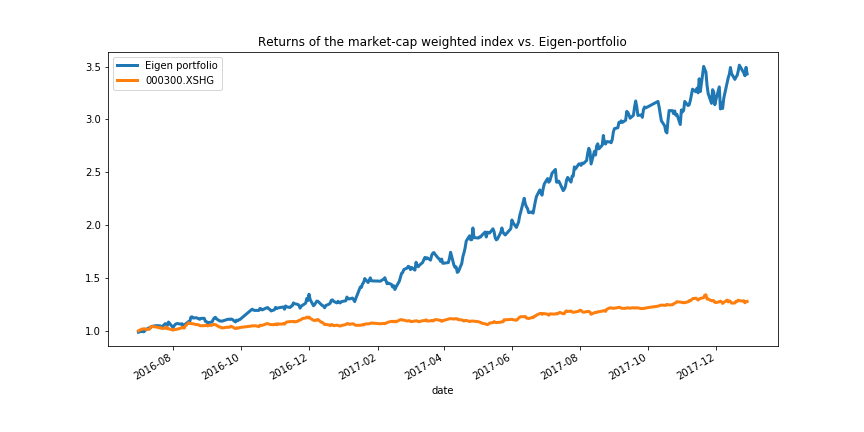
总结¶

本教程在很大程度上是对论文的复现，在实现的过程中也发现并总结了如下一些问题：

• PCA对数据非常敏感，数据加权、数据长度的选取以及缺失数据的处理都会极大得影响模型结果。
• 特征向量解释称组合权重，在逻辑上存在一定的问题，并且我们的处理方式是全额投资，然而如果特征向量存在加总和为负的情况，也就是特征组合是一个净空头头寸，那么将无法用全额投资的方式去分配权重。
• 论文的假设少量的特征向量选取有助于获得超过基准组合，这个在理论上没有依据。
• 特征向量如果作为风险因子，同样会存在上述我说的敏感性问题。

参考文献¶

1. Statistical Arbitrage in the U.S. Equities Market, Marco Avellaneda∗† and Jeong-Hyun Lee∗